Matlab: Ajusta tus datos a una distribución gaussiana como un experto

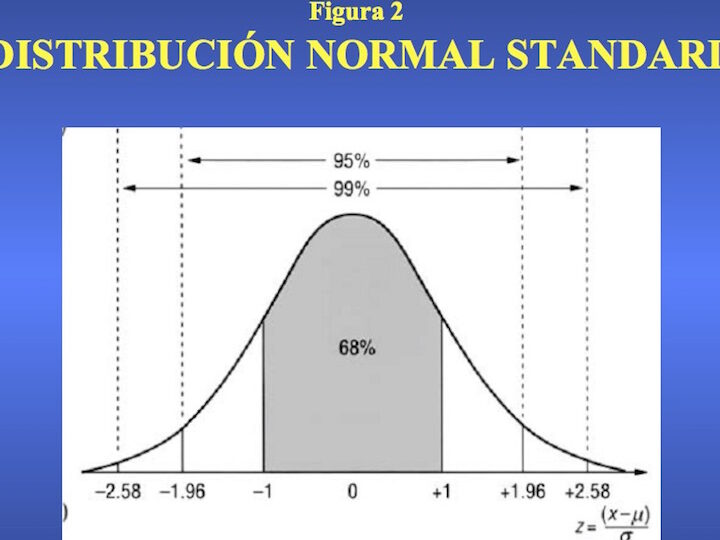
La distribución gaussiana, también conocida como distribución normal, es una de las distribuciones más importantes en estadística y probabilidad. Se utiliza para modelar una amplia variedad de fenómenos en diversos campos, desde la física hasta la econometría. Una de las tareas más comunes en el análisis de datos es ajustar los datos a una distribución gaussiana, lo cual permite realizar inferencias estadísticas y hacer pronósticos más precisos.

Aprenderás cómo utilizar Matlab para ajustar tus datos a una distribución gaussiana de manera eficiente y precisa. Te mostraremos paso a paso cómo cargar tus datos, generar una muestra de ajuste y utilizar las herramientas de Matlab para estimar los parámetros de la distribución gaussiana. También te daremos consejos prácticos sobre cómo validar tu modelo y realizar pruebas de bondad de ajuste. ¡Prepárate para convertirte en un experto en el ajuste de datos a una distribución gaussiana con Matlab!

Qué es una distribución gaussiana y por qué es importante en Matlab

Una distribución gaussiana, también conocida como distribución normal, es una de las distribuciones más comunes en estadística. Se caracteriza por tener una forma de campana simétrica y se utiliza para modelar una amplia variedad de fenómenos, desde el comportamiento de variables aleatorias hasta el ruido en las señales. En Matlab, ajustar datos a una distribución gaussiana es importante para analizar y comprender los datos de manera adecuada.

En Matlab, existen diversas herramientas y funciones disponibles para realizar el ajuste de datos a una distribución gaussiana. Estas herramientas permiten evaluar la bondad del ajuste, obtener parámetros como la media y la desviación estándar de la distribución, y realizar pruebas estadísticas para comparar diferentes distribuciones.

El ajuste de datos a una distribución gaussiana es especialmente útil en aplicaciones que requieren modelar variables aleatorias, como el análisis de datos experimentales, la predicción de valores futuros y la simulación de fenómenos.

En el siguiente apartado, exploraremos algunas de las herramientas y funciones más comunes que Matlab ofrece para ajustar datos a una distribución gaussiana.

Cuáles son las principales funciones y métodos en Matlab para ajustar datos a una distribución gaussiana

Matlab ofrece diversas funciones y métodos para ajustar datos a una distribución gaussiana de manera eficiente y precisa. Estas herramientas son ampliamente utilizadas en el análisis de datos y en la modelización de fenómenos naturales y sociales.

Función normfit

La función normfit es una de las principales herramientas de Matlab para el ajuste de datos a una distribución gaussiana. Esta función estima los parámetros de la distribución, es decir, la media y la desviación estándar, a partir de los datos de entrada.

El uso de normfit es bastante sencillo. Simplemente se debe pasar como argumento un vector con los datos a ajustar y la función devuelve la media y la desviación estándar estimadas.

Método de máxima verosimilitud

Otro enfoque ampliamente utilizado en Matlab para ajustar datos a una distribución gaussiana es el método de máxima verosimilitud. Este método busca encontrar los parámetros de la distribución que maximizan la probabilidad de observar los datos proporcionados.

El ajuste mediante máxima verosimilitud se realiza utilizando funciones específicas de Matlab, como mle, que permite estimar los parámetros de una distribución gaussiana a partir de los datos de entrada.

Comparación de ajustes

Una vez que se han obtenido los ajustes utilizando las diferentes herramientas de Matlab, es importante compararlos para evaluar su calidad y seleccionar el más adecuado.

Existen diversas medidas de bondad de ajuste que permiten comparar los resultados obtenidos, como el coeficiente de determinación (R^2) o el error cuadrático medio (MSE). Estas medidas se pueden calcular fácilmente utilizando funciones de Matlab como corrcoef o immse.

Además, es recomendable visualizar gráficamente el ajuste realizado utilizando la función normpdf de Matlab para representar la distribución gaussiana ajustada y compararla con los datos originales.

Cómo puedo visualizar gráficamente el ajuste de mis datos a una distribución gaussiana en Matlab

Una de las tareas más comunes en análisis de datos es ajustar una distribución gaussiana a un conjunto de datos. Matlab ofrece una manera sencilla de hacer esto y visualizar el resultado. Para empezar, necesitarás tener tus datos en un vector o matriz en Matlab. Luego, puedes utilizar la función "fitdist" para ajustar tus datos a una distribución gaussiana.

Una vez que hayas ajustado tus datos, puedes utilizar la función "pdf" para obtener los valores de densidad de probabilidad de la distribución gaussiana ajustada en distintos puntos. Luego, puedes utilizar la función "plot" para visualizar los datos originales y la distribución ajustada en un gráfico.

Para hacer esto, necesitarás crear un vector de valores x que cubra el rango de tus datos originales. Luego, debes utilizar la función "pdf" para obtener los valores de densidad de probabilidad correspondientes a estos valores x. Finalmente, puedes utilizar la función "plot" para visualizar los datos originales junto con la distribución ajustada.

Al visualizar el ajuste de tus datos a una distribución gaussiana, es importante tener en cuenta que el ajuste perfecto no siempre es posible. Es posible que tus datos no se ajusten perfectamente a una distribución gaussiana debido a ruido, errores de medición u otros factores. Sin embargo, visualizar el ajuste puede proporcionarte una idea general de qué tan bien se ajustan tus datos a una distribución gaussiana.

Cuál es el mejor enfoque para determinar si mis datos se ajustan bien a una distribución gaussiana en Matlab

En Matlab, existen diferentes enfoques para determinar si tus datos se ajustan a una distribución gaussiana. Uno de los métodos más utilizados es la prueba de chi-cuadrado. Esta prueba compara la distribución de los datos observados con la distribución esperada bajo la hipótesis nula de que los datos provienen de una distribución gaussiana.

Otro enfoque común es el uso de gráficos de probabilidad normal. Estos gráficos trazan los valores observados contra los valores esperados bajo una distribución gaussiana. Si los puntos se ajustan bien a una línea recta, esto indica un buen ajuste a una distribución gaussiana.

También puedes utilizar la prueba de Kolmogorov-Smirnov para determinar si tus datos siguen una distribución gaussiana. Esta prueba compara la función acumulativa de los datos observados con la función acumulativa de una distribución gaussiana. Si el valor p de la prueba es mayor que un umbral predefinido, puedes concluir que los datos se ajustan a una distribución gaussiana.

Es importante tener en cuenta que estos métodos son solo herramientas estadísticas y no proporcionan una prueba definitiva de ajuste a una distribución gaussiana. Siempre es recomendable combinar estos enfoques con un análisis visual de los datos y el conocimiento del contexto del problema.

Cómo puedo interpretar los coeficientes del ajuste de una distribución gaussiana en Matlab

Al ajustar nuestros datos a una distribución gaussiana en Matlab, obtenemos una serie de coeficientes que nos ayudan a interpretar el ajuste realizado. Estos coeficientes nos dan información valiosa sobre la media, la desviación estándar y otros parámetros de la distribución ajustada.

El primer coeficiente que debemos tener en cuenta es la media (μ), que representa el valor promedio de la distribución gaussiana ajustada. Este valor nos indica el punto central de la distribución y nos permite realizar comparaciones con datos observados o teóricos.

Otro coeficiente importante es la desviación estándar (σ), que indica la dispersión de los datos respecto a la media. Una desviación estándar mayor implica una distribución más amplia y dispersa, mientras que una desviación estándar menor indica una distribución más concentrada alrededor de la media.

Además de la media y la desviación estándar, existen otros coeficientes que podemos obtener al ajustar nuestros datos a una distribución gaussiana en Matlab. Por ejemplo, podemos obtener la amplitud de la distribución (A), que nos indica la altura máxima de la curva ajustada. También podemos obtener la posición del máximo (x0), que representa el valor de la variable independiente en el cual se alcanza la altura máxima de la distribución.

La interpretación de estos coeficientes nos permite comprender mejor nuestros datos y realizar análisis más detallados. Por ejemplo, si encontramos que la media es mayor que un valor de referencia, podemos concluir que nuestros datos tienden a ser mayores en promedio. Del mismo modo, si la desviación estándar es pequeña, podemos inferir que nuestros datos son más consistentes y menos dispersos.

Cuáles son los desafíos comunes al ajustar datos a una distribución gaussiana en Matlab y cómo puedo superarlos

Ajustar datos a una distribución gaussiana puede ser un desafío, especialmente cuando se trabaja con grandes conjuntos de datos en Matlab. Uno de los desafíos comunes es determinar los parámetros necesarios para el ajuste, como la media y la desviación estándar.

Una forma de superar este desafío es utilizando métodos de estimación de parámetros, como el método de máxima verosimilitud. Este método busca encontrar los valores de los parámetros que maximizan la probabilidad de observar los datos dados. Matlab ofrece funciones integradas, como 'mle', que facilitan este proceso.

Otro desafío común es evaluar la bondad del ajuste. Un simple gráfico de los datos y la distribución ajustada puede ayudar a identificar discrepancias. Matlab ofrece herramientas gráficas, como 'histfit', que permiten visualizar el ajuste y comparar los datos reales con la distribución gaussiana ajustada.

Además, es importante tener en cuenta que los datos pueden contener valores atípicos que afecten el ajuste. Matlab proporciona funciones para detectar y manejar valores atípicos, como 'isoutlier' y 'trimmean', respectivamente.

Al ajustar datos a una distribución gaussiana en Matlab, es importante considerar los desafíos de determinar los parámetros necesarios, evaluar la bondad del ajuste y manejar valores atípicos. Utilizando herramientas y funciones integradas en Matlab, como métodos de estimación de parámetros y funciones gráficas, puedes superar estos desafíos y ajustar tus datos como un experto.

Hay alguna herramienta adicional en Matlab que pueda ayudarme a ajustar datos a una distribución gaussiana de manera más eficiente

¡Absolutamente! Matlab ofrece una herramienta muy útil llamada "Curve Fitting Toolbox", que te permitirá ajustar tus datos a una distribución gaussiana de manera rápida y precisa. Esta herramienta incluye funciones y métodos especializados para el análisis de datos y el ajuste de curvas.

Con la "Curve Fitting Toolbox" podrás importar tus datos directamente desde archivos de Excel o desde tu espacio de trabajo en Matlab. Además, podrás visualizar tus datos en diferentes formatos, como gráficos de dispersión o histogramas, lo que facilitará la comprensión y el análisis de tus datos.

Una vez que hayas importado tus datos, podrás utilizar las funciones de ajuste de la "Curve Fitting Toolbox" para encontrar la mejor distribución gaussiana que se ajuste a tus datos. Estas funciones te permitirán ajustar los parámetros de la distribución gaussiana, como la media y la desviación estándar, para obtener un ajuste óptimo.

Además, la "Curve Fitting Toolbox" también te ofrece opciones avanzadas para evaluar la calidad del ajuste, como la generación de gráficos de residuos y la realización de pruebas de bondad de ajuste. Estas herramientas te ayudarán a verificar la confiabilidad de tu ajuste y a tomar decisiones basadas en evidencias estadísticas.

Si deseas ajustar tus datos a una distribución gaussiana de manera eficiente y precisa, la "Curve Fitting Toolbox" de Matlab es la herramienta ideal para ti. Con sus funciones y opciones avanzadas, podrás realizar análisis de datos y ajustes de curvas de una manera más profesional y confiable.

Existe alguna alternativa a la distribución gaussiana para ajustar datos en Matlab

Si bien la distribución gaussiana es ampliamente utilizada para ajustar datos en Matlab, existen algunas alternativas que pueden ser igualmente efectivas en determinados casos. Una opción popular es la distribución de Poisson, que se utiliza cuando estamos trabajando con datos discretos y queremos modelar eventos raros. También podemos utilizar la distribución exponencial, que es útil cuando estamos estudiando el tiempo entre eventos.

Otra alternativa es la distribución de Cauchy, que es adecuada para modelar fenómenos con colas pesadas, es decir, donde hay una alta probabilidad de obtener valores extremadamente alejados de la media. La distribución de Weibull también puede ser utilizada para ajustar datos que siguen un patrón de crecimiento o decaimiento.

Si los datos que estamos analizando no se ajustan bien a una distribución gaussiana, es recomendable explorar otras opciones como la distribución de Poisson, exponencial, Cauchy o Weibull, dependiendo de las características de nuestros datos.

Qué precauciones debo tener en cuenta al ajustar datos a una distribución gaussiana en Matlab para garantizar resultados precisos

Al ajustar datos a una distribución gaussiana en Matlab, es importante tener en cuenta ciertas precauciones que nos ayudarán a obtener resultados precisos. En primer lugar, es fundamental realizar una exploración visual de los datos para identificar cualquier posible desviación de la distribución normal. Esto nos permitirá decidir si es apropiado utilizar una distribución gaussiana para ajustar nuestros datos.

Otra precaución importante es tener en cuenta el tamaño de la muestra. En general, cuanto mayor sea el tamaño de la muestra, más precisa será la estimación de los parámetros de la distribución gaussiana. Por lo tanto, es recomendable trabajar con conjuntos de datos lo suficientemente grandes como para garantizar resultados robustos.

Antes de ajustar los datos, también es recomendable realizar una prueba de bondad de ajuste para evaluar la idoneidad de la distribución gaussiana. Esto se puede hacer utilizando pruebas estadísticas como la prueba de Kolmogorov-Smirnov o la prueba de Anderson-Darling.

Una vez que hayamos determinado que la distribución gaussiana es apropiada para nuestros datos, podemos proceder con el ajuste. Matlab ofrece diversas funciones y herramientas para llevar a cabo esta tarea, como la función "fitdist" para ajustar una distribución a los datos y la función "mle" para estimar los parámetros de la distribución.

Es importante mencionar que, aunque podemos ajustar nuestros datos a una distribución gaussiana, esto no garantiza que los datos se distribuyan exactamente de manera normal. Siempre debemos tener en cuenta que el ajuste es solo una aproximación y que existirán desviaciones en algunos casos.

Al ajustar datos a una distribución gaussiana en Matlab, debemos tener en cuenta la exploración visual de los datos, el tamaño de la muestra, realizar pruebas de bondad de ajuste y utilizar las herramientas adecuadas que nos proporciona Matlab. Además, es fundamental recordar que el ajuste es solo una aproximación y que siempre habrá desviaciones en algunos casos.

Cómo puedo utilizar el ajuste de una distribución gaussiana en Matlab para resolver problemas específicos en análisis de datos o modelado estadístico

Matlab es una herramienta poderosa para el análisis de datos y el modelado estadístico. Una técnica comúnmente utilizada en estos campos es el ajuste de datos a una distribución gaussiana. La distribución gaussiana, también conocida como distribución normal, es ampliamente utilizada debido a su fácil interpretación y su capacidad para describir muchos fenómenos naturales.

El ajuste de datos a una distribución gaussiana nos permite modelar y comprender mejor nuestros datos, así como realizar predicciones y tomar decisiones basadas en la distribución de probabilidad resultante. En Matlab, el ajuste de datos a una distribución gaussiana se puede lograr utilizando varias funciones y técnicas.

Ajuste de datos utilizando la función "fitdist"

Una forma común de ajustar datos a una distribución gaussiana en Matlab es utilizando la función "fitdist". Esta función permite ajustar los datos a una variedad de distribuciones, incluyendo la distribución gaussiana. Para ajustar los datos a una distribución gaussiana, debemos utilizar la sintaxis "fitdist(datos, 'normal')", donde "datos" es la muestra de datos que deseamos ajustar.

El resultado de la función "fitdist" es un objeto de ajuste que contiene información sobre los parámetros estimados de la distribución gaussiana ajustada. Podemos acceder a estos parámetros utilizando las funciones de acceso proporcionadas por el objeto de ajuste.

Evaluación del ajuste utilizando pruebas de bondad de ajuste

Una vez que hayamos ajustado nuestros datos a una distribución gaussiana, es importante evaluar la calidad del ajuste. Podemos hacer esto utilizando pruebas de bondad de ajuste, que nos permiten determinar si los datos siguen una distribución gaussiana o si hay desviaciones significativas.

En Matlab, existen varias pruebas de bondad de ajuste disponibles, incluyendo la prueba de Kolmogorov-Smirnov y la prueba de Chi-cuadrado. Estas pruebas comparan la distribución observada de los datos con la distribución teórica ajustada y nos proporcionan una medida de la desviación entre las dos. Cuanto menor sea el valor p obtenido de estas pruebas, mayor será la evidencia en contra del ajuste.

Visualización del ajuste utilizando gráficos

Además de las pruebas de bondad de ajuste, también es útil visualizar el ajuste de los datos a la distribución gaussiana utilizando gráficos. En Matlab, podemos hacer esto trazando un histograma de los datos y superponiendo la curva de la distribución gaussiana ajustada.

Para trazar el histograma, podemos utilizar la función "histogram" y para trazar la curva de la distribución gaussiana ajustada, podemos utilizar la función "plot". Al superponer estas dos visualizaciones, podemos ver cómo se ajusta la distribución gaussiana a los datos y evaluar visualmente la calidad del ajuste. Esto nos ayuda a identificar posibles desviaciones y anomalías en nuestros datos.

Preguntas frecuentes (FAQ)

1. ¿Qué es una distribución gaussiana?

La distribución gaussiana, también conocida como distribución normal, es una función matemática que describe una curva simétrica en forma de campana. Es ampliamente utilizada en estadística para modelar datos continuos y se caracteriza por su media y desviación estándar.

2. ¿Cómo puedo ajustar mis datos a una distribución gaussiana en Matlab?

En Matlab puedes utilizar la función "fitdist" del toolbox de estadísticas para ajustar tus datos a una distribución gaussiana. Esta función devuelve los parámetros estimados de la distribución, como la media y la desviación estándar.

3. ¿Cuál es la importancia de ajustar datos a una distribución gaussiana?

Ajustar datos a una distribución gaussiana puede ayudarte a entender mejor tus datos y realizar inferencias estadísticas más precisas. Además, muchas técnicas estadísticas asumen que los datos siguen una distribución normal, por lo que el ajuste a una distribución gaussiana puede ser útil para aplicar estas técnicas correctamente.

4. ¿Cuáles son las principales herramientas en Matlab para trabajar con distribuciones gaussianas?

En Matlab, aparte de la función "fitdist" mencionada anteriormente, puedes utilizar el toolbox de estadísticas para realizar cálculos relacionados con distribuciones gaussianas, como generar números aleatorios a partir de una distribución normal o calcular probabilidades y percentiles.

5. ¿Qué medidas de bondad de ajuste puedo utilizar para evaluar qué tan bien se ajustan mis datos a una distribución gaussiana en Matlab?

En Matlab puedes utilizar diversas medidas de bondad de ajuste, como la prueba de Kolmogorov-Smirnov, la prueba de Chi-cuadrado y el criterio de información de Akaike (AIC), para evaluar qué tan bien se ajustan tus datos a una distribución gaussiana.