
Cómo resolver mecanismos planos con MATLAB: ejercicios y métodos
Los mecanismos planos son elementos fundamentales en el diseño de máquinas y estructuras. Estos sistemas, con una geometría y movimiento limitados a un plano, son ampliamente utilizados en diversos campos como la ingeniería mecánica, la robótica y la arquitectura. Resolver los problemas asociados a estos mecanismos puede ser un desafío, pero gracias a herramientas como MATLAB, es posible simplificar y acelerar el proceso.
Exploraremos cómo utilizar MATLAB para resolver problemas de mecanismos planos. Veremos ejercicios prácticos y métodos específicos que nos permitirán modelar y analizar diferentes tipos de mecanismos. Desde la cinemática hasta la dinámica de los sistemas, descubriremos cómo aprovechar el poder de MATLAB para obtener soluciones precisas y eficientes. Si estás interesado en aprender más sobre este tema, ¡sigue leyendo!
- Cuáles son los conceptos básicos para resolver mecanismos planos con MATLAB
- Qué tipos de ejercicios se pueden resolver utilizando MATLAB para mecanismos planos
- Cuál es el método más eficiente para resolver mecanismos planos con MATLAB
- Existen paquetes de herramientas disponibles en MATLAB para resolver mecanismos planos de manera más rápida
- Cómo se puede representar gráficamente un mecanismo plano utilizando MATLAB
- Cuáles son los errores comunes al resolver mecanismos planos con MATLAB y cómo evitarlos
- Es posible simular el movimiento de un mecanismo plano en tiempo real utilizando MATLAB
- Cómo se pueden agregar restricciones y límites en la resolución de mecanismos planos con MATLAB
- Cuáles son las ventajas de utilizar una herramienta como MATLAB en la resolución de mecanismos planos en comparación con otros métodos manuales
- Existe alguna comunidad en línea donde se compartan ejercicios y soluciones de mecanismos planos resueltos con MATLAB
-
Preguntas frecuentes (FAQ)
- 1. ¿Qué es MATLAB?
- 2. ¿Para qué se utiliza MATLAB en la resolución de mecanismos planos?
- 3. ¿Cuáles son los métodos más comunes para resolver mecanismos planos con MATLAB?
- 4. ¿Es necesario tener conocimientos previos en programación para utilizar MATLAB en la resolución de mecanismos planos?
- 5. ¿Dónde puedo encontrar ejercicios y ejemplos de resolución de mecanismos planos con MATLAB?
Cuáles son los conceptos básicos para resolver mecanismos planos con MATLAB
Para resolver mecanismos planos con MATLAB, es importante comprender los conceptos básicos de cinemática y dinámica de los mecanismos. La cinemática se encarga de estudiar los movimientos y las relaciones geométricas entre los elementos del mecanismo, mientras que la dinámica se enfoca en las fuerzas y momentos que actúan sobre ellos.
En cuanto a la cinemática, es necesario familiarizarse con conceptos como posición, velocidad y aceleración. La posición se refiere a la ubicación de cada elemento del mecanismo en un momento dado, la velocidad es la tasa de cambio de la posición y la aceleración es la tasa de cambio de la velocidad.
Para representar el movimiento en MATLAB, se utilizan variables simbólicas para representar las variables de posición, velocidad y aceleración. Estas variables se pueden definir utilizando la función syms de MATLAB.
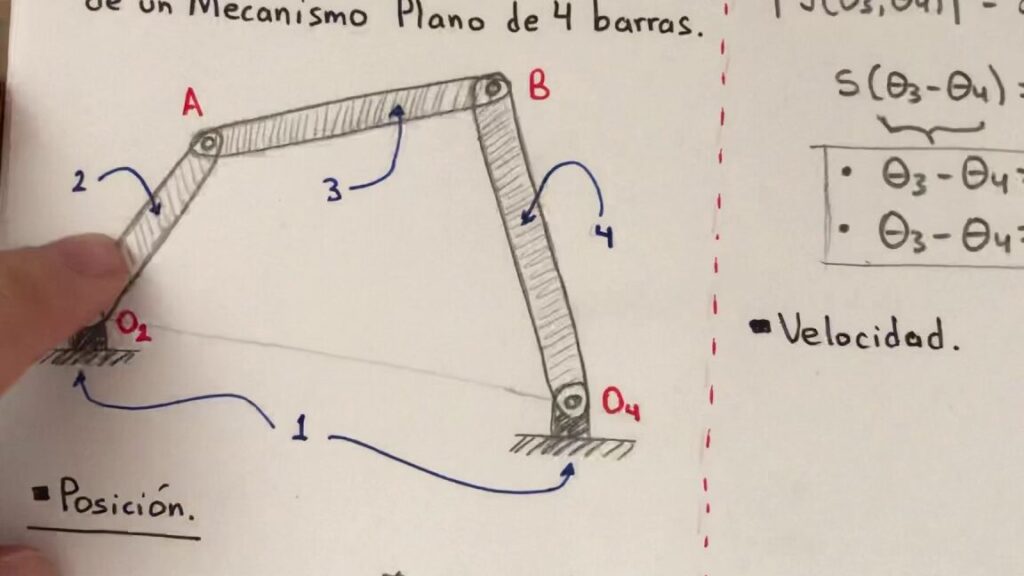
Además, es importante entender los tipos de mecanismos planos, como el mecanismo de cuatro barras, el mecanismo de doble manivela y el mecanismo de manivela-corredera. Cada uno de estos mecanismos tiene características distintas y requiere diferentes enfoques para su resolución en MATLAB.
En cuanto a la dinámica de los mecanismos, se deben considerar las fuerzas y momentos que actúan sobre los elementos del mecanismo. Estas fuerzas y momentos pueden ser causados por la gravedad, la fricción o la interacción con otros objetos. Para modelar estas fuerzas en MATLAB, se utilizan ecuaciones de equilibrio y leyes físicas como la ley de Newton.
Los conceptos básicos para resolver mecanismos planos con MATLAB incluyen la comprensión de la cinemática y la dinámica de los mecanismos, el uso de variables simbólicas para representar las variables de posición, velocidad y aceleración, y la consideración de las fuerzas y momentos que actúan sobre los elementos del mecanismo.
Qué tipos de ejercicios se pueden resolver utilizando MATLAB para mecanismos planos
En MATLAB puedes resolver una amplia variedad de ejercicios relacionados con mecanismos planos. Algunos ejemplos incluyen calcular las velocidades y aceleraciones de las diferentes partes del mecanismo, calcular las fuerzas y momentos en las articulaciones, determinar las trayectorias y posiciones de los puntos en el mecanismo, analizar los impactos y colisiones, y simular el comportamiento dinámico del mecanismo bajo diferentes condiciones. Además, MATLAB también te permite visualizar los resultados de manera gráfica para ayudarte a entender mejor el comportamiento del mecanismo.
Para resolver estos ejercicios en MATLAB, es necesario utilizar las herramientas de análisis y simulación disponibles en la plataforma. Estas herramientas incluyen funciones para calcular derivadas, integrales, y resolver ecuaciones diferenciales, así como funciones para modelar y simular el comportamiento de los mecanismos. Además, MATLAB también cuenta con una gran cantidad de recursos y documentación disponibles que te ayudarán a resolver toda clase de ejercicios relacionados con mecanismos planos.
Algunos de los métodos más comunes utilizados en MATLAB para resolver ejercicios de mecanismos planos incluyen el método de las fuerzas, el método de la cinemática inversa, el método de la dinámica inversa, y el método de la cinemática directa. Estos métodos te permiten analizar y resolver diferentes aspectos del mecanismo, como las fuerzas y momentos en las articulaciones, las velocidades y aceleraciones de las partes del mecanismo, las trayectorias y posiciones de los puntos en el mecanismo, y el comportamiento dinámico del mecanismo bajo diferentes condiciones.
Método de las fuerzas
El método de las fuerzas es utilizado para calcular las fuerzas y momentos en las articulaciones de un mecanismo plano. Para utilizar este método en MATLAB, es necesario empezar por definir las ecuaciones de equilibrio de fuerzas y momentos para cada articulación del mecanismo. Estas ecuaciones se pueden obtener utilizando las leyes de Newton y las ecuaciones de equilibrio de fuerzas y momentos.
Una vez que se tienen las ecuaciones de equilibrio, se pueden utilizar las funciones disponibles en MATLAB para resolver las ecuaciones y obtener los valores de las fuerzas y momentos en las articulaciones. Estas funciones te permiten ingresar las ecuaciones de equilibrio, así como las condiciones y restricciones del mecanismo, y obtienen los resultados de manera automática. Además, MATLAB también te permite visualizar los resultados en forma gráfica para ayudarte a entender mejor el comportamiento del mecanismo.
El método de las fuerzas es utilizado en MATLAB para calcular las fuerzas y momentos en las articulaciones de un mecanismo plano. Este método utiliza las ecuaciones de equilibrio de fuerzas y momentos para cada articulación, y utiliza las funciones disponibles en MATLAB para resolver las ecuaciones y obtener los resultados. Además, MATLAB también te permite visualizar los resultados en forma gráfica para ayudarte a entender mejor el comportamiento del mecanismo.
Método de la cinemática inversa
El método de la cinemática inversa es utilizado para determinar las posiciones y trayectorias de los puntos en un mecanismo plano. Este método es útil cuando se conoce la posición deseada de un punto en el mecanismo, y se desea determinar las posiciones y trayectorias de los demás puntos en el mecanismo que están relacionados con ese punto.
Para utilizar el método de la cinemática inversa en MATLAB, es necesario empezar por definir las ecuaciones de posición y trayectoria para cada punto en el mecanismo. Estas ecuaciones se pueden obtener utilizando las relaciones geométricas y trigonométricas entre los diferentes puntos en el mecanismo.
Una vez que se tienen las ecuaciones de posición y trayectoria, se pueden utilizar las funciones disponibles en MATLAB para resolver las ecuaciones y obtener los valores de las posiciones y trayectorias de los puntos en el mecanismo. Estas funciones te permiten ingresar las ecuaciones de posición y trayectoria, así como las condiciones y restricciones del mecanismo, y obtienen los resultados de manera automática. Además, MATLAB también te permite visualizar los resultados en forma gráfica para ayudarte a entender mejor el comportamiento del mecanismo.
El método de la cinemática inversa es utilizado en MATLAB para determinar las posiciones y trayectorias de los puntos en un mecanismo plano. Este método utiliza las ecuaciones de posición y trayectoria para cada punto en el mecanismo, y utiliza las funciones disponibles en MATLAB para resolver las ecuaciones y obtener los resultados. Además, MATLAB también te permite visualizar los resultados en forma gráfica para ayudarte a entender mejor el comportamiento del mecanismo.
Cuál es el método más eficiente para resolver mecanismos planos con MATLAB
Al utilizar MATLAB para resolver mecanismos planos, existen varios métodos disponibles. Sin embargo, el método más eficiente es el método de Newton-Raphson. Este método utiliza aproximaciones sucesivas para encontrar la solución de un sistema de ecuaciones no lineales. En el contexto de los mecanismos planos, el método de Newton-Raphson se utiliza para resolver las ecuaciones cinemáticas que describen el movimiento de los distintos elementos del mecanismo.
El método de Newton-Raphson se basa en la idea de iterar hacia una solución mediante la mejora continua de una aproximación inicial. En cada iteración, el método calcula una nueva aproximación basada en la derivada de las ecuaciones cinemáticas. Esto permite una convergencia rápida y precisa hacia la solución final.
El método de Newton-Raphson se implementa fácilmente en MATLAB utilizando funciones de optimización y resolución de sistemas de ecuaciones. En particular, la función 'fsolve' de MATLAB es ampliamente utilizada para resolver sistemas de ecuaciones no lineales, lo que lo convierte en la herramienta ideal para implementar el método de Newton-Raphson en el contexto de los mecanismos planos.
El método de Newton-Raphson es el enfoque más eficiente para resolver mecanismos planos con MATLAB. Su capacidad para converger rápidamente hacia la solución final lo convierte en la elección preferida para resolver las ecuaciones cinemáticas que describen el movimiento de los mecanismos planos. Al utilizar la función 'fsolve' de MATLAB, la implementación del método de Newton-Raphson es sencilla y accesible para los usuarios de MATLAB.
Existen paquetes de herramientas disponibles en MATLAB para resolver mecanismos planos de manera más rápida
Uno de los paquetes de herramientas más utilizados para resolver mecanismos planos con MATLAB es el Toolbox de Robótica. Este paquete de software permite a los ingenieros y diseñadores simular y analizar diversos mecanismos planos, como brazos robóticos y sistemas de transmisión de movimiento.
El Toolbox de Robótica proporciona una amplia gama de funciones y algoritmos que permiten a los usuarios modelar la cinemática y dinámica de los mecanismos planos. Además, también ofrece la posibilidad de realizar análisis de singularidades y optimización de trayectorias.
Otro paquete de herramientas útil para resolver mecanismos planos con MATLAB es el Toolbox de Mecanismos y Dinámica de Maquinaria. Este paquete está diseñado específicamente para analizar y simular mecanismos planos en movimiento.
El Toolbox de Mecanismos y Dinámica de Maquinaria ofrece una amplia gama de funciones y algoritmos que permiten a los usuarios modelar y analizar la cinemática y dinámica de los mecanismos planos. Además, también proporciona herramientas para realizar análisis de fuerzas y momentos, así como análisis de estabilidad y rendimiento.
Además de estos paquetes de herramientas, MATLAB también ofrece una amplia gama de funciones y algoritmos incorporados que permiten a los usuarios resolver mecanismos planos de manera eficiente. Estas funciones y algoritmos pueden utilizarse de forma independiente o combinarse con los paquetes de herramientas mencionados anteriormente para obtener resultados más precisos y completos.
MATLAB ofrece una amplia variedad de paquetes de herramientas y funciones incorporadas que permiten a los ingenieros y diseñadores resolver mecanismos planos de manera más rápida y eficiente. Ya sea utilizando el Toolbox de Robótica, el Toolbox de Mecanismos y Dinámica de Maquinaria o las funciones y algoritmos incorporados en MATLAB, los usuarios pueden simular, analizar y optimizar diversos mecanismos planos con facilidad.
Cómo se puede representar gráficamente un mecanismo plano utilizando MATLAB
En MATLAB, se pueden representar gráficamente mecanismos planos utilizando la función plot. Esta función permite graficar puntos y líneas en un plano cartesiano. Para representar un mecanismo, se deben definir las coordenadas de los puntos y las líneas que lo conforman. Luego, se utiliza la función plot para dibujar cada elemento. Además, se pueden personalizar los colores, estilos y etiquetas de los elementos gráficos. Con esta técnica, es posible visualizar de manera clara y precisa los movimientos y configuraciones del mecanismo.
Una vez que se ha creado el gráfico del mecanismo, es posible agregar anotaciones y etiquetas a los puntos y líneas utilizando las funciones text y annotation. Estas funciones permiten agregar texto, flechas y otros elementos decorativos al gráfico para facilitar su comprensión. Además, se pueden utilizar diferentes vistas y ajustes de cámara para explorar el mecanismo desde distintos ángulos. Al utilizar MATLAB para representar gráficamente un mecanismo plano, se pueden obtener visualizaciones detalladas y personalizadas que facilitan el análisis y diseño del mismo.
Cuáles son los errores comunes al resolver mecanismos planos con MATLAB y cómo evitarlos
Resolver mecanismos planos en MATLAB puede ser un proceso complicado, especialmente cuando se cometen errores comunes. Uno de los errores más comunes es no tener en cuenta las restricciones de movimiento de los eslabones del mecanismo. Es importante recordar que cada eslabón está sujeto a restricciones específicas y no se puede mover libremente en cualquier dirección.
Otro error común es no considerar las condiciones de contorno adecuadas. Esto puede llevar a resultados incorrectos o inconsistentes. Es importante definir claramente las condiciones iniciales y límites para resolver con precisión los mecanismos planos en MATLAB.
Además, no analizar correctamente la función de transferencia del mecanismo puede ser otro error común. Es crucial comprender cómo se relacionan las variables de entrada y salida del mecanismo para poder modelarlo adecuadamente en MATLAB.
Otro error común es no considerar el efecto de las fuerzas externas sobre el mecanismo. Es importante tener en cuenta las fuerzas aplicadas al sistema, ya que pueden tener un impacto significativo en el resultado de la simulación.
Por último, no utilizar los métodos y funciones apropiados de MATLAB también puede ser un error común. MATLAB ofrece una amplia gama de funciones y herramientas para resolver mecanismos planos, como la función "solve" para resolver ecuaciones algebraicas o la función "ode45" para resolver ecuaciones diferenciales. Es importante utilizar las herramientas adecuadas para obtener resultados precisos.
Al resolver mecanismos planos con MATLAB, es importante evitar errores comunes como no tener en cuenta las restricciones de movimiento, no considerar las condiciones de contorno adecuadas, no analizar correctamente la función de transferencia, no considerar las fuerzas externas y no utilizar los métodos y funciones apropiados de MATLAB. Al evitar estos errores, podremos obtener resultados precisos y confiables en nuestras simulaciones de mecanismos planos.
Es posible simular el movimiento de un mecanismo plano en tiempo real utilizando MATLAB
El software MATLAB es una poderosa herramienta que permite resolver de manera eficiente y precisa problemas de ingeniería, como la simulación de mecanismos planos. Con MATLAB, es posible modelar y simular el movimiento de un mecanismo plano en tiempo real, lo que facilita el análisis y diseño de sistemas mecánicos complejos.
Existen diferentes métodos y técnicas para resolver mecanismos planos con MATLAB. Algunos de los más comunes incluyen el método de las fuerzas y el método de las velocidades. Estos métodos permiten determinar las posiciones, velocidades y aceleraciones de las distintas partes del mecanismo a lo largo del tiempo.
Uno de los ejercicios más comunes al resolver mecanismos planos con MATLAB es determinar las posiciones de las diferentes partes del mecanismo en función del tiempo. Esto se logra utilizando las ecuaciones de movimiento del mecanismo, las cuales pueden ser obtenidas mediante el análisis de fuerzas y velocidades.
Una vez obtenidas las ecuaciones de movimiento, se pueden utilizar técnicas numéricas, como la integración numérica o el método de Runge-Kutta, para resolverlas y obtener las posiciones de las diferentes partes del mecanismo en función del tiempo. Estas posiciones pueden ser representadas gráficamente utilizando MATLAB, lo que facilita la visualización y comprensión del movimiento del mecanismo.
Otro ejercicio común es determinar las velocidades y aceleraciones de las diferentes partes del mecanismo en función del tiempo. Esto es especialmente útil para analizar el rendimiento y la eficiencia de un mecanismo, así como para identificar posibles problemas o limitaciones en su diseño.
La simulación de mecanismos planos con MATLAB ofrece numerosas ventajas, como la capacidad de resolver problemas de manera eficiente y precisa, la posibilidad de visualizar el movimiento del mecanismo en tiempo real, y la facilidad de análisis y diseño de sistemas mecánicos complejos. Con los diferentes métodos y técnicas disponibles, así como los ejercicios prácticos que se pueden realizar, MATLAB se convierte en una herramienta invaluable para aquellos que trabajan en el campo de la ingeniería mecánica.
Cómo se pueden agregar restricciones y límites en la resolución de mecanismos planos con MATLAB
En la resolución de mecanismos planos con MATLAB, es fundamental agregar restricciones y límites para obtener resultados precisos y realistas. Afortunadamente, MATLAB ofrece diversas opciones para implementar restricciones en la solución de mecanismos planos.
Una de las formas más comunes de agregar restricciones es mediante la función "constraint". Esta función permite definir restricciones geométricas, como la longitud de un enlace o el ángulo entre dos enlaces. Además de las restricciones geométricas, también es posible agregar restricciones dinámicas, como la velocidad o la aceleración máxima permitida.
Por ejemplo, supongamos que tenemos un mecanismo plano con tres enlaces conectados por tres juntas. Podemos agregar una restricción para limitar la longitud del enlace superior utilizando la función "constraint" de la siguiente manera:
constraint('L1', )
Esta restricción asegura que la longitud del enlace superior (L1) sea menor o igual a 1 unidad. De esta manera, podemos evitar configuraciones inestables o físicamente imposibles en la solución del mecanismo.
Otra forma de agregar restricciones es mediante la función "boundary". Esta función permite establecer límites para las variables de diseño del mecanismo, como las longitudes de los enlaces o los ángulos entre ellos.
Por ejemplo, supongamos que queremos limitar la longitud del enlace inferior (L3) a un valor entre 0.5 y 1 unidad. Podemos utilizar la función "boundary" de la siguiente manera:
boundary('L3', 0.5, 1)
Con esta restricción, aseguramos que la longitud del enlace inferior (L3) se encuentre dentro del rango especificado durante la resolución del mecanismo.
Agregar restricciones y límites en la resolución de mecanismos planos con MATLAB es esencial para obtener resultados precisos y realistas. Ya sea mediante la función "constraint" para restricciones geométricas y dinámicas, o mediante la función "boundary" para establecer límites en las variables de diseño, MATLAB ofrece diversas opciones para ajustar y controlar la solución de mecanismos planos.
Cuáles son las ventajas de utilizar una herramienta como MATLAB en la resolución de mecanismos planos en comparación con otros métodos manuales
Una de las principales ventajas de utilizar MATLAB en la resolución de mecanismos planos es la capacidad de automatizar los cálculos y reducir errores humanos. MATLAB ofrece una amplia gama de funciones y herramientas específicas para el análisis y diseño de mecanismos que facilitan el proceso.
Otra ventaja importante es la posibilidad de visualizar los resultados de manera gráfica. MATLAB permite representar los mecanismos planos en forma de diagramas cinemáticos, lo que facilita la comprensión y análisis de su movimiento.
Además, MATLAB ofrece una gran flexibilidad en la modelización y simulación de mecanismos planos. Se pueden implementar fácilmente diferentes algoritmos y métodos para resolver problemas específicos, lo que permite adaptar el software a las necesidades y requerimientos de cada caso.
Por último, el uso de MATLAB en la resolución de mecanismos planos es ampliamente utilizado en la industria y la academia. Esto significa que hay una gran cantidad de recursos y documentación disponible, lo que facilita el aprendizaje y la aplicación de esta herramienta.
Existe alguna comunidad en línea donde se compartan ejercicios y soluciones de mecanismos planos resueltos con MATLAB
Sí, en la comunidad de MATLAB existen varios recursos donde se comparten ejercicios y soluciones de mecanismos planos resueltos. Uno de los lugares más populares es el foro de MATLAB, donde los usuarios pueden publicar sus preguntas y recibir ayuda de otros miembros de la comunidad. Además, también se encuentran disponibles varios sitios web y blogs especializados en MATLAB, donde se pueden encontrar ejercicios resueltos y métodos para resolver mecanismos planos. Estos recursos son muy útiles para aquellos que están aprendiendo MATLAB y desean obtener una comprensión más profunda de cómo resolver mecanismos planos utilizando este software.
Los ejercicios y soluciones compartidos en estas comunidades en línea pueden ser una excelente forma de practicar y desarrollar habilidades en la resolución de mecanismos planos con MATLAB. Al trabajar en ejercicios reales y revisar las soluciones propuestas por otros usuarios, se puede aprender de diferentes enfoques y técnicas utilizadas en la resolución de problemas. Además, al participar en estas comunidades en línea, se puede establecer contacto con otros entusiastas de MATLAB y compartir ideas y experiencias relacionadas con la resolución de mecanismos planos. Esto puede ser especialmente beneficioso para aquellos que están comenzando en el campo y buscan ampliar su red de contactos profesionales.
Además de los ejercicios y soluciones compartidos por los miembros de la comunidad, también existen numerosos tutoriales y recursos educativos disponibles en línea que pueden ayudar a comprender los conceptos y métodos utilizados en la resolución de mecanismos planos con MATLAB. Estos tutoriales suelen incluir explicaciones detalladas y ejemplos de código que muestran cómo implementar algoritmos y métodos específicos en MATLAB. Al seguir estos tutoriales paso a paso, se puede adquirir una comprensión más sólida de los fundamentos de la resolución de mecanismos planos y cómo aplicarlos utilizando el software MATLAB.
Sitios web y blogs especializados en MATLAB para la resolución de mecanismos planos
- Blog de MATLAB: en este blog oficial de MATLAB, se pueden encontrar artículos, tutoriales y ejemplos de mecanismos planos resueltos utilizando MATLAB.
- MathWorks File Exchange: en este sitio, los usuarios pueden compartir sus scripts y funciones de MATLAB relacionados con la resolución de mecanismos planos.
- GitHub: en esta plataforma de desarrollo colaborativo, también se pueden encontrar repositorios con scripts y proyectos de mecanismos planos resueltos utilizando MATLAB.
Estos son solo algunos ejemplos de los recursos disponibles en línea para aquellos interesados en resolver mecanismos planos con MATLAB. Sin embargo, es importante destacar que estos recursos son complementarios a la práctica y el estudio independiente. Es fundamental dedicar tiempo y esfuerzo para comprender los conceptos y métodos utilizados en la resolución de mecanismos planos, y utilizar estos recursos como guías y referencias en el proceso de aprendizaje.
Existen diversas comunidades en línea donde se comparten ejercicios y soluciones de mecanismos planos resueltos con MATLAB. Estos recursos pueden ser de gran ayuda para aquellos que están aprendiendo MATLAB y desean practicar y desarrollar habilidades en la resolución de mecanismos planos. Además, también existen sitios web y blogs especializados en MATLAB que proporcionan tutoriales y ejemplos de código para ayudar en el proceso de aprendizaje. Es importante aprovechar estas oportunidades de aprendizaje, pero también es fundamental dedicar tiempo y esfuerzo a la práctica y el estudio independiente para adquirir una comprensión sólida de los fundamentos de la resolución de mecanismos planos con MATLAB.
Preguntas frecuentes (FAQ)
1. ¿Qué es MATLAB?
MATLAB es un lenguaje de programación y un entorno de desarrollo diseñado para realizar cálculos numéricos y análisis de datos.
2. ¿Para qué se utiliza MATLAB en la resolución de mecanismos planos?
MATLAB se utiliza en la resolución de mecanismos planos para realizar simulaciones, resolver ecuaciones y graficar resultados.
3. ¿Cuáles son los métodos más comunes para resolver mecanismos planos con MATLAB?
Algunos métodos comunes para resolver mecanismos planos con MATLAB son el método gráfico, el método analítico y el método numérico.
4. ¿Es necesario tener conocimientos previos en programación para utilizar MATLAB en la resolución de mecanismos planos?
No es necesario tener conocimientos previos en programación, aunque tenerlos puede facilitar el uso y la comprensión de MATLAB.
5. ¿Dónde puedo encontrar ejercicios y ejemplos de resolución de mecanismos planos con MATLAB?
Existen diferentes recursos en línea, como tutoriales, libros y sitios web especializados, donde se pueden encontrar ejercicios y ejemplos de resolución de mecanismos planos con MATLAB.
Deja una respuesta








Artículos que podrían interesarte