Código MATLAB: Resuelve una ecuación de tercer grado fácilmente
Las ecuaciones de tercer grado son uno de los desafíos matemáticos más complejos de resolver. A menudo requieren de conocimientos avanzados de álgebra y cálculo, así como de métodos numéricos sofisticados. Sin embargo, con la ayuda de programas de computadora como MATLAB, resolver una ecuación de tercer grado se vuelve mucho más accesible y eficiente.
Exploraremos cómo utilizar MATLAB para resolver ecuaciones de tercer grado de manera sencilla y rápida. Veremos paso a paso el proceso de introducir la ecuación en el programa, aplicar métodos numéricos y obtener una solución aproximada. Además, discutiremos algunas consideraciones importantes a tener en cuenta al resolver este tipo de ecuaciones y cómo interpretar los resultados obtenidos en MATLAB.
¿Qué verás en este artículo?
- Qué es una ecuación de tercer grado en matemáticas y cómo se resuelve
- Cuál es la fórmula general para resolver una ecuación de tercer grado
- Cuáles son los pasos para resolver una ecuación de tercer grado utilizando MATLAB
- Existen funciones predefinidas en MATLAB para resolver ecuaciones de tercer grado
- Cuáles son los posibles métodos numéricos para resolver ecuaciones de tercer grado en MATLAB
- Cómo se visualizan los resultados de la solución de una ecuación de tercer grado en MATLAB
- Cuáles son las precauciones a tener en cuenta al resolver ecuaciones de tercer grado en MATLAB
- Qué hacer si MATLAB no encuentra una solución para una ecuación de tercer grado
- Es posible resolver ecuaciones de tercer grado con coeficientes complejos en MATLAB
- Cómo se puede verificar la solución obtenida para una ecuación de tercer grado en MATLAB
- Cuáles son las aplicaciones prácticas de resolver ecuaciones de tercer grado en MATLAB
- Dónde puedo encontrar ejemplos y ejercicios para practicar la resolución de ecuaciones de tercer grado en MATLAB
-
Preguntas frecuentes (FAQ)
- 1. ¿Qué es una ecuación de tercer grado?
- 2. ¿Qué métodos se pueden utilizar para resolver una ecuación de tercer grado?
- 3. ¿Cómo puedo resolver una ecuación de tercer grado en MATLAB?
- 4. ¿Puedo resolver una ecuación de tercer grado con coeficientes complejos en MATLAB?
- 5. ¿Qué debo hacer si la función "roots" devuelve un error en MATLAB?
Qué es una ecuación de tercer grado en matemáticas y cómo se resuelve
Una ecuación de tercer grado es una ecuación algebraica en la que la variable desconocida está elevada a la tercera potencia. Por ejemplo, una ecuación de tercer grado puede ser de la forma ax^3 + bx^2 + cx + d = 0, donde a, b, c y d son coeficientes dados.
Resolver una ecuación de tercer grado puede ser un desafío, pero con la ayuda del MATLAB, podemos simplificar el proceso. MATLAB es un lenguaje de programación y un entorno de desarrollo que facilita la resolución de problemas matemáticos de manera rápida y eficiente.
Pasos para resolver una ecuación de tercer grado en MATLAB
- Paso 1: Definir los coeficientes de la ecuación
- Paso 2: Crear una función en MATLAB para la ecuación de tercer grado
- Paso 3: Utilizar la función "roots" de MATLAB para obtener las raíces de la ecuación
- Paso 4: Mostrar las soluciones obtenidas
En el primer paso, es importante definir los coeficientes a, b, c y d de la ecuación de tercer grado. Estos coeficientes pueden ser números reales o complejos, dependiendo del problema que estemos tratando de resolver.
En el segundo paso, creamos una función en MATLAB que represente la ecuación de tercer grado. Esta función toma los coeficientes como parámetros de entrada y devuelve el valor de la ecuación evaluada en un punto dado.
En el tercer paso, utilizamos la función "roots" de MATLAB para encontrar las raíces de la ecuación. La función "roots" devuelve un vector con las soluciones de la ecuación, que pueden ser números reales o complejos.
Finalmente, en el cuarto paso, mostramos las soluciones obtenidas para la ecuación de tercer grado. Esto nos permite verificar si las soluciones son correctas y resolver problemas matemáticos más complejos.
Resolver una ecuación de tercer grado en MATLAB es más sencillo utilizando la función "roots". Esta función nos permite obtener las raíces de la ecuación y resolver problemas matemáticos de manera eficiente.
Cuál es la fórmula general para resolver una ecuación de tercer grado
La fórmula general para resolver una ecuación de tercer grado es una herramienta clave en el campo de las matemáticas. Esta fórmula nos permite encontrar las raíces de una ecuación polinómica de tercer grado, también conocida como una ecuación cúbica.
La fórmula general se expresa de la siguiente manera:
x = (-b ± √(b^2 - 4ac - c^3))/(2a)
Donde a, b y c son coeficientes reales y x representa las raíces de la ecuación.
Es importante tener en cuenta que, en algunos casos, la fórmula general puede producir raíces complejas o repetidas. Sin embargo, también existen métodos alternativos para resolver ecuaciones cúbicas en estos casos.
A continuación, exploraremos cómo implementar esta fórmula general en MATLAB y resolver fácilmente una ecuación de tercer grado.
Cuáles son los pasos para resolver una ecuación de tercer grado utilizando MATLAB
Resolver una ecuación de tercer grado utilizando MATLAB puede ser bastante sencillo si se siguen los pasos correctos. A continuación, se detallarán los pasos necesarios para resolver este tipo de ecuaciones con esta herramienta.
Paso 1: Definir la ecuación
Lo primero que debemos hacer es definir la ecuación de tercer grado que deseamos resolver. Esto implica establecer los coeficientes de la ecuación y el término independiente, si lo hay. Por ejemplo, una ecuación de tercer grado podría estar escrita de la siguiente manera:
ax^3 + bx^2 + cx + d = 0
Paso 2: Utilizar la función "roots"
Una vez que tenemos nuestra ecuación definida, podemos utilizar la función "roots" de MATLAB para encontrar las raíces de la ecuación. Esta función toma como argumento un vector que contiene los coeficientes de la ecuación y devuelve las soluciones reales y complejas.
Paso 3: Mostrar las raíces obtenidas
Una vez que hemos utilizado la función "roots" para encontrar las raíces de la ecuación de tercer grado, podemos mostrar las soluciones obtenidas en la ventana de comandos de MATLAB. Esto nos permitirá verificar si las soluciones son correctas y analizar los resultados obtenidos.
Paso 4: Verificar las soluciones
Es importante verificar las soluciones obtenidas utilizando la función "roots" para asegurarnos de que son correctas. Podemos hacer esto sustituyendo las raíces encontradas en la ecuación original y comprobando que ambas partes de la ecuación sean iguales.
Paso 5: Interpretar los resultados
Una vez que hemos verificado las soluciones obtenidas, podemos interpretar los resultados. Esto implica analizar si las soluciones son reales o complejas, y determinar si hay raíces múltiples o repetidas. Esta interpretación nos ayudará a comprender mejor la naturaleza de la ecuación de tercer grado.
Utilizar MATLAB para resolver una ecuación de tercer grado puede ser una tarea relativamente sencilla si se siguen los pasos adecuados. Definir la ecuación, utilizar la función "roots", mostrar las soluciones obtenidas, verificar las soluciones y finalmente interpretar los resultados son los pasos necesarios para resolver este tipo de ecuaciones utilizando esta herramienta.
Existen funciones predefinidas en MATLAB para resolver ecuaciones de tercer grado
Una de las grandes ventajas de MATLAB es la gran cantidad de funciones predefinidas que facilitan la resolución de problemas matemáticos. En el caso de las ecuaciones de tercer grado, no es necesario desarrollar un código complejo desde cero. MATLAB nos proporciona una función específica para resolver este tipo de ecuaciones.
La función se llama roots, y su sintaxis es muy sencilla. Solo tenemos que proporcionar los coeficientes de la ecuación de tercer grado y MATLAB se encargará de encontrar las soluciones reales e imaginarias. A continuación, vamos a ver cómo utilizar esta función en un ejemplo práctico.
Ejemplo de uso de la función roots
Supongamos que tenemos la siguiente ecuación de tercer grado:
2x^3 - 7x^2 + 5x - 3 = 0
Para resolver esta ecuación utilizando la función roots, primero debemos definir los coeficientes:
a = ;
A continuación, simplemente llamamos a la función roots pasando como argumento el vector de coeficientes:
soluciones = roots(a);
El resultado de esta línea de código será un vector con las soluciones reales e imaginarias de la ecuación. En este caso, obtendremos tres soluciones:
soluciones =
2.5248
-0.2624 + 0.6571i
-0.2624 - 0.6571i
La solución real es 2.5248, mientras que las soluciones imaginarias son -0.2624 + 0.6571i y -0.2624 - 0.6571i. Con la función roots de MATLAB, resolver ecuaciones de tercer grado se convierte en una tarea sencilla y rápida.
Cuando necesitemos resolver ecuaciones de tercer grado en MATLAB, no es necesario desarrollar un código complejo desde cero. Podemos utilizar la función predefinida roots para obtener las soluciones de manera rápida y precisa. Esto nos permite ahorrar tiempo y esfuerzo, centrándonos en el análisis de los resultados obtenidos.
Cuáles son los posibles métodos numéricos para resolver ecuaciones de tercer grado en MATLAB
En MATLAB, existen diferentes métodos numéricos que pueden utilizarse para resolver ecuaciones de tercer grado. Algunos de los métodos más comunes son:
Método gráfico
Este método consiste en graficar la función y encontrar las intersecciones con el eje x. Estas intersecciones corresponderán a las raíces de la ecuación.
Método de Newton-Raphson
Este método utiliza iteraciones sucesivas para encontrar una aproximación de la raíz de la ecuación. Comienza con una estimación inicial y utiliza la fórmula de Newton-Raphson para refinar la aproximación en cada iteración.
Método de Horner
Este método utiliza la división sintética para simplificar la ecuación de tercer grado a una ecuación de segundo grado. Luego, se pueden utilizar métodos numéricos para resolver la ecuación de segundo grado.
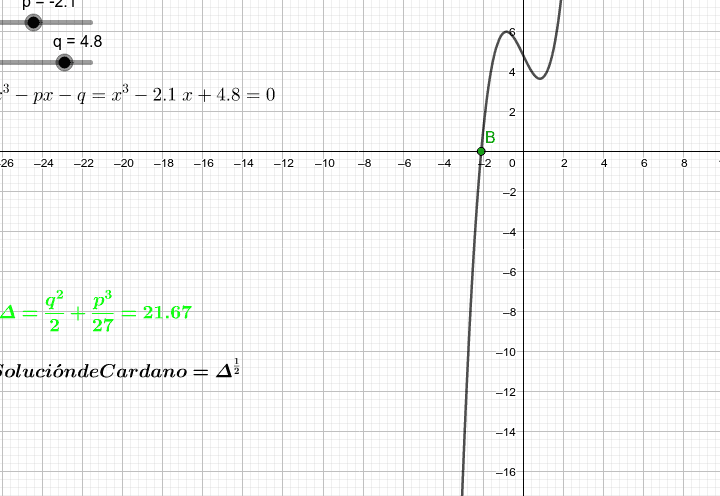
Método de Cardano
Este método utiliza una fórmula especial desarrollada por el matemático italiano Gerolamo Cardano para encontrar las raíces de la ecuación de tercer grado. La fórmula implica la resolución de una ecuación de segundo grado y una ecuación de primer grado.
Estos son solo algunos de los métodos numéricos que pueden utilizarse para resolver ecuaciones de tercer grado en MATLAB. Cada método tiene sus propias ventajas y desventajas, y la elección del método dependerá de la naturaleza de la ecuación y los requisitos del problema.
Cómo se visualizan los resultados de la solución de una ecuación de tercer grado en MATLAB
La visualización de los resultados de la solución de una ecuación de tercer grado en MATLAB puede ser muy útil para comprender mejor los resultados obtenidos. MATLAB ofrece varias herramientas y funciones que permiten representar gráficamente las soluciones de ecuaciones de tercer grado de manera clara y concisa.
Una de las formas más comunes de visualizar los resultados es mediante la gráfica de la función polinómica resultante de la ecuación de tercer grado. Esto se puede lograr utilizando la función "plot" de MATLAB, que permite trazar la curva de la función en un rango de valores.
Otra forma de visualizar los resultados es mediante el uso de gráficos de dispersión. En este caso, se pueden trazar los puntos correspondientes a las soluciones de la ecuación de tercer grado en un sistema de coordenadas cartesianas.
Utilizando la función plot para visualizar las soluciones de una ecuación de tercer grado
Para visualizar las soluciones de una ecuación de tercer grado utilizando la función "plot" de MATLAB, primero debemos obtener los valores correspondientes a la función polinómica resultante. Para esto, podemos utilizar la función "polyval", que evalúa un polinomio en un punto dado.
Una vez que tenemos los valores de la función polinómica, podemos utilizar la función "plot" para trazar la curva de la función en un rango de valores. Por ejemplo, si queremos trazar la curva en el rango , podemos hacerlo de la siguiente manera:
x = -10:0.1:10;
y = polyval(coeficientes, x);
plot(x, y);
Donde "coeficientes" es un vector que contiene los coeficientes del polinomio resultante de la ecuación de tercer grado.
Utilizando gráficos de dispersión para visualizar las soluciones de una ecuación de tercer grado
Para visualizar las soluciones de una ecuación de tercer grado utilizando gráficos de dispersión, podemos utilizar la función "scatter" de MATLAB. Esta función permite trazar los puntos correspondientes a las soluciones en un sistema de coordenadas cartesianas.
Primero, debemos obtener los valores de las soluciones de la ecuación de tercer grado. Una vez que tenemos estos valores, podemos utilizar la función "scatter" para trazar los puntos en el sistema de coordenadas. Por ejemplo:
x = soluciones_reales;
y = zeros(size(soluciones_reales));
scatter(x, y, 'filled', 'r');
Donde "soluciones_reales" es un vector que contiene los valores reales de las soluciones de la ecuación de tercer grado. Los puntos se representan en color rojo y se rellenan.
MATLAB ofrece varias opciones para visualizar los resultados de la solución de una ecuación de tercer grado de manera clara y concisa. Ya sea utilizando la función "plot" para trazar la curva de la función polinómica resultante, o utilizando gráficos de dispersión para trazar los puntos correspondientes a las soluciones.
Cuáles son las precauciones a tener en cuenta al resolver ecuaciones de tercer grado en MATLAB
Al resolver ecuaciones de tercer grado en MATLAB, es importante tener en cuenta algunas precauciones para evitar errores. En primer lugar, debemos asegurarnos de que la ecuación esté correctamente escrita y que todos los términos estén presentes. Además, es esencial definir de forma adecuada las variables y los coeficientes necesarios para el cálculo.
Es recomendable también verificar que los datos de entrada sean válidos, evitando así divisiones por cero o errores numéricos. Además, es importante considerar que MATLAB utiliza una notación específica para las operaciones matemáticas, por lo que debemos tener en cuenta estas reglas al escribir nuestra ecuación.
Otra precaución importante es comprobar que el sistema de ecuaciones esté bien condicionado. Si el sistema es mal condicionado, los resultados pueden ser inexactos o poco fiables. Por lo tanto, es recomendable utilizar métodos numéricos más estables, como el método de Newton-Raphson o el método de Horner, para evitar este problema.
Por último, es necesario recordar que las soluciones de una ecuación de tercer grado pueden ser complejas. En MATLAB, es posible obtener tanto las soluciones reales como las soluciones complejas utilizando la función "roots". Sin embargo, es importante tener en cuenta que los resultados pueden ser complicados de interpretar si se obtienen soluciones complejas.
Qué hacer si MATLAB no encuentra una solución para una ecuación de tercer grado
En ocasiones, al trabajar con MATLAB, nos encontramos con situaciones en las que al resolver una ecuación de tercer grado, el software no es capaz de encontrar una solución. Esto puede ser frustrante, pero no te preocupes, hay alternativas que puedes probar para solucionar este problema.
1. Verifica la sintaxis de la ecuación
Es posible que el error se encuentre en la forma en que has escrito la ecuación en MATLAB. Revisa cuidadosamente la sintaxis, asegurándote de que todos los términos estén escritos correctamente y que los operadores matemáticos estén en el lugar correcto.
2. Ajusta los parámetros de la función solve
La función solve de MATLAB tiene varios parámetros que puedes ajustar para ayudar a encontrar la solución de la ecuación. Puedes especificar un rango de valores para las variables, cambiar el número de soluciones que se deben encontrar o indicar restricciones adicionales que deben cumplirse.
3. Prueba otros métodos de resolución
Además de la función solve, MATLAB ofrece otros métodos de resolución de ecuaciones, como fsolve y vpasolve. Estos métodos pueden ser más eficientes para ciertos tipos de ecuaciones o para problemas específicos.
4. Simplifica la ecuación
Si la ecuación de tercer grado es muy compleja, podría ser útil simplificarla antes de intentar resolverla. Puedes utilizar herramientas de álgebra simbólica, como la función simplify, para reducir la ecuación a una forma más manejable.
5. Consulta recursos adicionales
Si después de probar todas estas opciones aún no encuentras una solución para tu ecuación de tercer grado, no te desesperes. Hay numerosos recursos en línea, como foros de programación y grupos de discusión, donde puedes buscar ayuda adicional de expertos en MATLAB y matemáticas.
Recuerda que resolver ecuaciones de tercer grado puede ser un desafío incluso para los programadores experimentados, pero con paciencia y persistencia, puedes encontrar una solución para tu problema.
Es posible resolver ecuaciones de tercer grado con coeficientes complejos en MATLAB
En MATLAB, es posible resolver ecuaciones de tercer grado con coeficientes complejos de forma sencilla. Gracias a las funciones incorporadas en MATLAB, los cálculos se simplifican enormemente, permitiéndonos obtener rápidamente las soluciones de dicha ecuación.
Para resolver una ecuación de tercer grado en MATLAB, primero debemos asegurarnos de tener instalado el paquete Symbolic Math Toolbox, el cual nos proporciona las herramientas necesarias para realizar cálculos simbólicos.
Una vez que contamos con dicho paquete, podemos utilizar la función solve para resolver la ecuación. Esta función nos permite encontrar las raíces de una ecuación polinómica, incluyendo las de tercer grado.
¿Cómo utilizar la función solve en MATLAB?
El uso básico de la función solve consiste en especificar la ecuación que deseamos resolver y las variables que queremos encontrar. Por ejemplo, si queremos resolver la ecuación:
3x^3 + 2x^2 - 5x + 1 = 0
Podemos escribir el siguiente código:
syms x
eqn = 3x^3 + 2x^2 - 5x + 1 == 0;
solutions = solve(eqn, x);
En este caso, hemos definido la variable simbólica x utilizando la función syms. Luego, hemos especificado la ecuación que queremos resolver y la hemos asignado a la variable eqn. Finalmente, utilizamos la función solve para encontrar las soluciones de la ecuación y las guardamos en la variable solutions.
Es importante destacar que, en el caso de ecuaciones de tercer grado, es posible obtener hasta tres soluciones diferentes. En caso de que existan soluciones complejas, MATLAB también nos las mostrará de forma sencilla, utilizando la notación i para representar la unidad imaginaria.
Resolver ecuaciones de tercer grado con coeficientes complejos en MATLAB es realmente sencillo gracias a la función solve. Solo necesitamos tener instalado el paquete Symbolic Math Toolbox y utilizar esta función para encontrar las soluciones de la ecuación que deseamos resolver.
Cómo se puede verificar la solución obtenida para una ecuación de tercer grado en MATLAB
Una vez que hayas utilizado el comando polyval para calcular las raíces de una ecuación de tercer grado en MATLAB, es importante poder verificar que la solución obtenida es correcta. Para hacer esto, puedes utilizar la función polyval nuevamente, pero esta vez insertando los valores de las raíces calculadas en lugar de la variable. Luego, puedes comparar los resultados obtenidos con cero, ya que si la ecuación original es igual a cero, se espera que los resultados también lo sean. Si los resultados son cercanos a cero, se puede considerar que la solución obtenida es válida y precisa.
Por ejemplo, si tienes una ecuación de tercer grado de la forma ax^3 + bx^2 + cx + d = 0, y has calculado las raíces utilizando el comando polyval, puedes verificar la solución de la siguiente manera:
% Supongamos que las raíces calculadas son r1, r2 y r3
resultado1 = polyval(, r1);
resultado2 = polyval(, r2);
resultado3 = polyval(, r3);
% Verificar si los resultados son cercanos a cero
if abs(resultado1) < 1e-10 && abs(resultado2) < 1e-10 && abs(resultado3) < 1e-10
disp('La solución es válida');
else
disp('La solución no es válida');
end
De esta manera, puedes asegurarte de que los valores obtenidos para las raíces de la ecuación de tercer grado son correctos. Es importante recordar que, debido a limitaciones numéricas, es posible que los resultados no sean exactamente cero, pero si son lo suficientemente cercanos, se pueden considerar como solución válida.
Cuáles son las aplicaciones prácticas de resolver ecuaciones de tercer grado en MATLAB
Resolver ecuaciones de tercer grado en MATLAB puede tener varias aplicaciones prácticas en campos como la ingeniería, la física y las matemáticas aplicadas. Estas ecuaciones son de gran importancia ya que permiten modelar y resolver problemas complejos que no se pueden abordar utilizando métodos algebraicos tradicionales.
Por ejemplo, en ingeniería estructural, resolver una ecuación de tercer grado puede ayudar a determinar la carga crítica que puede soportar una estructura en particular. En física, estas ecuaciones pueden utilizarse para modelar sistemas dinámicos y predecir su comportamiento en diferentes condiciones.
En matemáticas aplicadas, la resolución de ecuaciones de tercer grado es esencial para analizar curvas cúbicas y encontrar puntos críticos o soluciones óptimas en problemas de optimización.
Resolver ecuaciones de tercer grado en MATLAB es una herramienta poderosa que permite abordar problemas complejos en diversas disciplinas y enriquecer la comprensión de fenómenos físicos y matemáticos.
Dónde puedo encontrar ejemplos y ejercicios para practicar la resolución de ecuaciones de tercer grado en MATLAB
Si estás buscando ejemplos y ejercicios para practicar la resolución de ecuaciones de tercer grado en MATLAB, estás en el lugar indicado. Hay muchas fuentes en línea donde puedes encontrar problemas prácticos y soluciones en código MATLAB.
Una opción es buscar en foros y comunidades en línea dedicadas a la programación y MATLAB. En estos espacios, los usuarios suelen compartir ejercicios y soluciones, y también puedes hacer preguntas si tienes dudas.
Otra opción es consultar libros y tutoriales de MATLAB que cubran el tema de la resolución de ecuaciones de tercer grado. Estos recursos a menudo incluyen ejemplos y ejercicios prácticos, junto con explicaciones detalladas paso a paso.
En algunos casos, las universidades y los cursos en línea también proporcionan materiales de práctica para la resolución de ecuaciones de tercer grado en MATLAB. Puedes revisar los recursos disponibles de tu institución educativa o buscar en plataformas de aprendizaje en línea.
Además, hay sitios web dedicados específicamente a la programación en MATLAB que ofrecen ejercicios y desafíos en diferentes niveles de dificultad. Estos sitios te permiten poner a prueba tus habilidades de resolución de ecuaciones de tercer grado y mejorar tus conocimientos en el proceso.
Recuerda que la práctica es fundamental para dominar cualquier habilidad de programación, por lo que te animo a que busques ejemplos y ejercicios de resolución de ecuaciones de tercer grado en MATLAB y los resuelvas por ti mismo. Cuanto más practiques, más confianza ganarás en tu capacidad para resolver este tipo de problemas.
Preguntas frecuentes (FAQ)
1. ¿Qué es una ecuación de tercer grado?
Una ecuación de tercer grado es una ecuación algebraica en la que el término de mayor grado es el cubo de la variable desconocida.
2. ¿Qué métodos se pueden utilizar para resolver una ecuación de tercer grado?
Algunos métodos para resolver una ecuación de tercer grado son: el método de Cardano-Tartaglia, el método de Horner y el método de factorización.
3. ¿Cómo puedo resolver una ecuación de tercer grado en MATLAB?
En MATLAB, puedes utilizar la función "roots" para resolver una ecuación de tercer grado. Simplemente ingresa los coeficientes de la ecuación y la función devolverá las raíces.
4. ¿Puedo resolver una ecuación de tercer grado con coeficientes complejos en MATLAB?
Sí, MATLAB es capaz de resolver ecuaciones de tercer grado con coeficientes complejos. La función "roots" devolverá las raíces complejas si es necesario.
5. ¿Qué debo hacer si la función "roots" devuelve un error en MATLAB?
Si la función "roots" devuelve un error, puede ser debido a que la ecuación no tiene solución real o porque los coeficientes son incorrectos. Verifica los coeficientes y asegúrate de que la ecuación tenga solución antes de resolverla.
Calcula la derivada por definición en MATLAB: paso a paso
Añade columna al inicio de un vector en MATLAB: guía fácil y rápida
Conviértete en un experto: Cómo crear un array de 0 a 1 en MATLAB
Encuentra fácilmente el valor mínimo en un array cell en MATLAB
Abre tus ficheros de forma rápida y sencilla con este script de Matlab
Elimina archivos de una carpeta con Matlab de forma sencilla
Elevar 10 a un número en MATLAB: La guía definitiva sin complicaciones
Aprende fácilmente a calcular las soluciones de una función con MATLAB
Calcula la media de un vector en Matlab fácilmente paso a paso
Deja una respuesta
Artículos que podrían interesarte