Calcula los ceros en MATLAB: descubre cómo a partir de los polos

Los polos y los ceros son los componentes fundamentales en el análisis y diseño de sistemas de control. Los polos determinan la estabilidad y la respuesta transitoria del sistema, mientras que los ceros afectan la respuesta en frecuencia y la eliminación de errores de seguimiento o ruido.

La ubicación de los polos y los ceros en el plano complejo es crucial en el estudio de los sistemas de control. Los polos están relacionados con las singularidades que causan cambios en la respuesta del sistema, mientras que los ceros representan los ceros de la función transferencia y ayudan a modelar el comportamiento del sistema.

Es importante destacar que los polos y los ceros pueden ser complejos conjugados, y las propiedades y ubicación de estos puntos en el plano complejo tienen un impacto directo en el comportamiento del sistema en función del tiempo y la frecuencia.

Los ceros son valores que anulan la función transferencia en un sistema de control en MATLAB, y se utilizan en combinación con los polos para caracterizar y modelar el comportamiento de un sistema.

Cuál es la importancia de calcular los ceros en el análisis de sistemas en MATLAB

En el análisis de sistemas en MATLAB, el cálculo de los ceros es de vital importancia. Los ceros son las raíces del denominador de la función de transferencia de un sistema, y representan los puntos en los cuales la función se anula. Estos ceros nos ayudan a comprender el comportamiento del sistema y determinar su estabilidad. También nos permiten identificar las frecuencias de resonancia y los modos de vibración del sistema. Además, el cálculo de los ceros en MATLAB nos brinda la posibilidad de realizar ajustes y optimizaciones en nuestros sistemas, mejorando su rendimiento y eficiencia.

Cómo calcular los ceros de un sistema en MATLAB

En MATLAB, podemos calcular los ceros de un sistema utilizando la función zero(). Esta función nos permite encontrar las raíces del denominador de la función de transferencia de un sistema lineal. Para ello, simplemente debemos ingresar la función de transferencia del sistema como argumento de la función. Por ejemplo:

sys = tf(,);
zeros = zero(sys);

En este ejemplo, hemos definido la función de transferencia del sistema como (s^2 + 2s + 3)/(4s^2 + 5s + 6). Luego, utilizando la función zero(), hemos calculado los ceros del sistema y los hemos almacenado en la variable zeros. Podemos imprimir los ceros obtenidos utilizando la función disp(). Veamos:

disp(zeros);

Al ejecutar este código, obtendremos los ceros del sistema en la ventana de comandos de MATLAB.

Aplicaciones del cálculo de los ceros en MATLAB

El cálculo de los ceros en MATLAB tiene numerosas aplicaciones en el campo del análisis de sistemas y control. Algunas de estas aplicaciones incluyen:

• Estabilidad del sistema: los ceros nos permiten determinar la estabilidad de un sistema. Si todos los ceros tienen parte real negativa, el sistema es estable. Si alguno de los ceros tiene parte real positiva, el sistema es inestable.
• Respuesta en frecuencia: los ceros nos ayudan a comprender la respuesta en frecuencia de un sistema. Nos permiten identificar las frecuencias de resonancia y los modos de vibración del sistema.
• Ajuste y optimización del sistema: el cálculo de los ceros nos brinda la posibilidad de realizar ajustes y optimizaciones en nuestros sistemas. Podemos manipular los ceros para mejorar el rendimiento y eficiencia del sistema.

El cálculo de los ceros en MATLAB es esencial en el análisis de sistemas y control. Nos brinda información valiosa sobre la estabilidad, respuesta en frecuencia y posibilidades de ajuste de nuestros sistemas. Utilizando la función zero(), podemos calcular los ceros de un sistema de manera rápida y sencilla.

Cuáles son las diferentes formas de calcular los ceros en MATLAB

En MATLAB, existen varias formas de calcular los ceros de una función. La más común es utilizando la función roots(), que encuentra las raíces de un polinomio dado. Esta función devuelve un vector con todos los ceros.

Otra opción es utilizar el comando fzero(), que encuentra la raíz de una función no lineal utilizando el método de la secante. Este método requiere proporcionar un intervalo donde se encuentra la raíz.

Además, MATLAB cuenta con la función fminbnd(), que utiliza el método de la falsa posición para encontrar la raíz de una función en un intervalo determinado.

Por último, otra forma de calcular los ceros es utilizando el comando fsolve(), que encuentra las raíces de un sistema de ecuaciones no lineales. Este comando utiliza diferentes métodos iterativos, como el método de Newton o el método de la secante, para encontrar las soluciones.

MATLAB ofrece varias opciones para calcular los ceros de una función: roots(), fzero(), fminbnd() y fsolve(). Cada una de estas funciones tiene sus propias ventajas y desventajas, por lo que es importante elegir la más adecuada para cada caso.

Cómo se pueden representar gráficamente los ceros de una función en MATLAB

En MATLAB, se pueden representar gráficamente los ceros de una función utilizando la función zplane. Esta función permite visualizar tanto los ceros como los polos de una función en el plano complejo. Al representar los ceros de una función, se puede obtener información sobre la ubicación de las raíces de la función en el plano complejo.

Para utilizar la función zplane, es necesario tener los coeficientes de la función. Estos coeficientes pueden ser obtenidos a partir de la función de transferencia de un sistema, por ejemplo. Una vez que se tienen los coeficientes, se puede utilizar la función zplane para representar los ceros en el plano complejo.

La función zplane también permite especificar el rango de frecuencias a plotear, lo cual puede ser útil cuando se trabaja con sistemas de frecuencia variable. Además, se pueden personalizar los colores y las etiquetas de los gráficos generados por la función.

Utilizar la función zplane en MATLAB es una forma sencilla y eficaz de visualizar los ceros de una función en el plano complejo. Esto puede ser útil en el análisis y diseño de sistemas de control, procesamiento de señales y otras áreas de la ciencia y la ingeniería.

Cuál es la diferencia entre los ceros reales y los ceros complejos en MATLAB

En MATLAB, los ceros son los valores de entrada para los cuales la función resulta en cero. Existen dos tipos de ceros que se pueden encontrar en MATLAB: los ceros reales y los ceros complejos.

Ceros reales en MATLAB

Los ceros reales son los valores para los cuales la función es igual a cero. Estos ceros se representan como números reales en MATLAB y se pueden calcular mediante diversas técnicas, como el método de Newton-Raphson o el método de la secante.

Ceros complejos en MATLAB

Los ceros complejos son aquellos en los que la función resulta en cero, pero tienen una parte imaginaria. Estos ceros se representan como números complejos en MATLAB y también pueden calcularse utilizando diferentes métodos numéricos, como el método de la bisectriz o el método de la regla falsa.

Importancia de los ceros en MATLAB

Los ceros son fundamentales en MATLAB, ya que son útiles para encontrar soluciones de ecuaciones, identificar estabilidad en sistemas dinámicos y determinar la respuesta de un sistema lineal. Por tanto, el conocimiento y cálculo de los ceros es esencial para una amplia gama de aplicaciones en ingeniería y ciencias.

En MATLAB existen dos tipos de ceros: los ceros reales y los ceros complejos. Los ceros reales son aquellos en los que la función es igual a cero, mientras que los ceros complejos tienen una parte imaginaria. Ambos tipos de ceros son importantes para diversas aplicaciones en ingeniería y ciencias, y se pueden calcular utilizando diferentes métodos numéricos.

Qué métodos numéricos existen para calcular los ceros en MATLAB

Método de la función "roots"

Uno de los métodos más utilizados en MATLAB para calcular los ceros de una función es el método de la función "roots". Esta función permite encontrar las raíces de un polinomio y devuelve los valores numéricos de dichas raíces.

Método de la función "fzero"

Otro método muy utilizado es el de la función "fzero". Esta función permite encontrar las raíces de una función no lineal en un intervalo dado. El método utilizado por la función "fzero" se basa en la técnica de la secante y requiere proporcionar un punto inicial cercano a la raíz deseada.

Método de la función "solve"

En el caso de tener un sistema de ecuaciones no lineales, se puede utilizar la función "solve" de MATLAB. Esta función permite resolver sistemas de ecuaciones algebraicas y encontrar las soluciones numéricas para las variables desconocidas.

Método de la función "fsolve"

Similar al método anterior, la función "fsolve" permite resolver sistemas de ecuaciones no lineales. La diferencia radica en que la función "fsolve" utiliza un algoritmo de optimización basado en el método de Newton-Raphson para encontrar las soluciones numéricas.

Método de la función "eig"

Si se desea encontrar los ceros de una matriz, se puede utilizar la función "eig" de MATLAB. Esta función calcula los autovalores de una matriz y devuelve los valores numéricos correspondientes. Los autovalores son equivalentes a los ceros de un polinomio característico.

Método de la función "fminsearch"

Si se busca encontrar los mínimos de una función, se puede utilizar la función "fminsearch". Aunque no está diseñada específicamente para encontrar ceros, puede ser útil en casos donde el valor de la función en el cero es cercano a cero. La función "fminsearch" utiliza un algoritmo de búsqueda basado en la técnica del descenso más pronunciado.

Método de la función "vpasolve"

En el caso de necesitar calcular ceros para ecuaciones simbólicas, se puede utilizar la función "vpasolve" de MATLAB. Esta función permite encontrar soluciones numéricas para ecuaciones simbólicas y algebraicas. Es importante mencionar que la función "vpasolve" se basa en algoritmos numéricos y es especialmente útil para ecuaciones que no tienen una solución analítica.

Método de la función "solvepdeeig"

Si se trabaja con ecuaciones en derivadas parciales, se puede utilizar la función "solvepdeeig" para calcular los ceros de una ecuación de autovalores para un problema de valor propio. Esta función permite encontrar los autovalores y autovectores correspondientes a través de métodos numéricos.

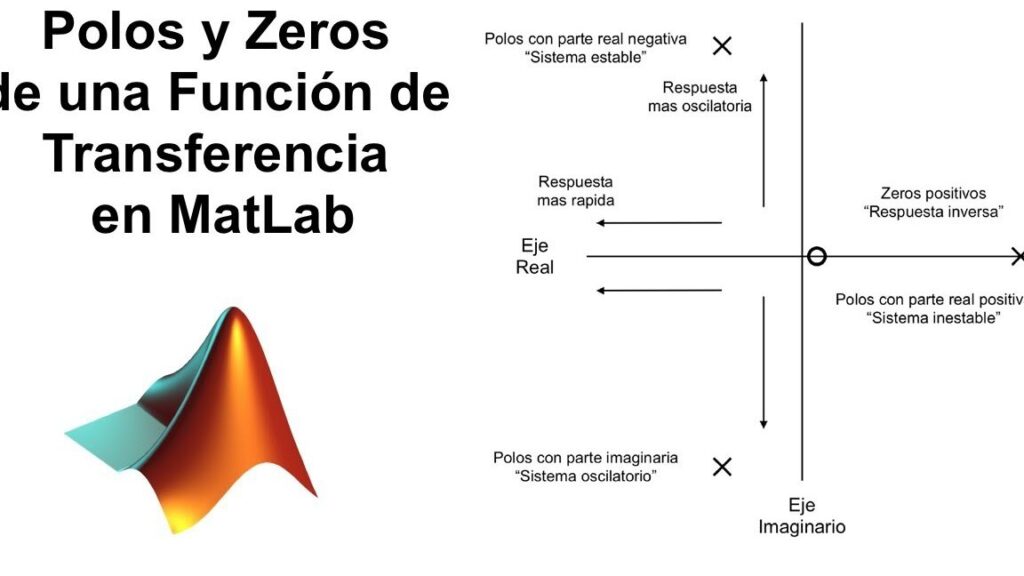
Cuál es la relación entre los ceros, los polos y la estabilidad de un sistema en MATLAB

Los ceros y los polos son conceptos fundamentales en el análisis de sistemas lineales en MATLAB. Los ceros son los valores de entrada que hacen que la función de transferencia sea igual a cero. Por otro lado, los polos son los valores de entrada que hacen que la función de transferencia sea infinita.

La posición de los ceros y los polos en el plano complejo determina la estabilidad del sistema. Si todos los polos están en el semiplano izquierdo, el sistema es estable. Si hay polos en el semiplano derecho, el sistema es inestable.

Los ceros y los polos también están relacionados entre sí. Si un cero y un polo tienen la misma ubicación en el plano complejo, se dice que hay una cancelación y el sistema se estabiliza. Si hay más ceros que polos en una ubicación, el sistema se amplifica en esa frecuencia. Por el contrario, si hay más polos que ceros, el sistema se atenúa en esa frecuencia.

En MATLAB, puedes calcular los ceros y los polos de un sistema utilizando la función tf2zp. Esta función toma la función de transferencia en forma de coeficientes y devuelve los ceros y los polos correspondientes.

Cómo calcular los ceros y los polos en MATLAB

Para calcular los ceros y los polos en MATLAB, primero debes definir la función de transferencia utilizando los coeficientes del numerador y el denominador. Luego, puedes utilizar la función tf2zp para obtener los ceros y los polos.

A continuación se muestra un ejemplo de cómo calcular los ceros y los polos de un sistema en MATLAB:

num = ; % Coeficientes del numerador
den = ; % Coeficientes del denominador

 = tf2zp(num, den); % Calcula los ceros, los polos y la ganancia

En este ejemplo, los coeficientes del numerador son y los coeficientes del denominador son . Después de llamar a la función tf2zp, los ceros se almacenarán en la variable z, los polos en la variable p y la ganancia en la variable k.

Una vez que hayas calculado los ceros y los polos, puedes utilizar esta información para analizar la estabilidad y el comportamiento del sistema en MATLAB.

Cuáles son las ventajas y desventajas de utilizar la función "roots" de MATLAB para calcular los ceros

Ventajas de utilizar la función "roots"

Una de las ventajas principales de utilizar la función "roots" de MATLAB para calcular los ceros de una función es su simplicidad y facilidad de uso. Con esta función, simplemente necesitas ingresar los coeficientes del polinomio y obtendrás de manera rápida y precisa los ceros correspondientes.

Otra ventaja es la eficiencia en el cómputo. La función "roots" utiliza algoritmos optimizados que permiten calcular los ceros de polinomios de forma eficiente, incluso para polinomios de grado elevado.

Además, la función "roots" proporciona una representación numérica de los ceros, lo que facilita el análisis y manipulación posterior de los mismos en otras operaciones matemáticas.

Desventajas de utilizar la función "roots"

A pesar de sus ventajas, la función "roots" también presenta ciertas limitaciones. Una de ellas es la sensibilidad a la precisión numérica. En algunos casos, la función puede generar resultados aproximados debido a errores de redondeo, lo que puede afectar la exactitud de los ceros calculados.

Otra desventaja es que la función "roots" solo calcula los ceros de un polinomio. Si se desea obtener los ceros de una función más compleja, como una función transcendental o una función racional, se requiere de otros métodos o algoritmos más avanzados.

Además, la función "roots" solo devuelve los ceros reales de un polinomio. Si se desean encontrar los ceros complejos, se necesita utilizar otras funciones o combinaciones de métodos.

A pesar de estas desventajas, la función "roots" sigue siendo una herramienta poderosa y útil para el cálculo de los ceros de polinomios en MATLAB, especialmente para polinomios simples y de grado moderado.

Existen casos en los que no se puedan calcular los ceros de una función en MATLAB

Al trabajar con funciones en MATLAB, es importante tener en cuenta que no siempre es posible calcular los ceros de una función de manera exacta. Esto se debe a que los ceros de una función son los valores de entrada que hacen que la función sea igual a cero.

Sin embargo, existen casos en los que no se puede determinar de forma precisa los ceros de una función. Esto puede ocurrir cuando la función es muy compleja o cuando los ceros son números complejos.

En estos casos, MATLAB ofrece diferentes métodos numéricos para aproximar los ceros de una función. Estos métodos, como el método de Newton-Raphson o el método de bisección, permiten obtener una estimación cercana de los ceros de una función, aunque no sean exactos.

Método de Newton-Raphson para aproximar los ceros de una función

El método de Newton-Raphson es un método iterativo que permite encontrar las raíces de una función. Para utilizar este método en MATLAB, es necesario proporcionar una función de entrada y una estimación inicial cercana al cero.

El método de Newton-Raphson utiliza la siguiente fórmula para encontrar una mejor aproximación del cero:

x = x - f(x)/f'(x)

Donde x es la estimación inicial, f(x) es la función evaluada en x y f'(x) es la derivada de la función evaluada en x.

Este proceso se repite hasta obtener una aproximación suficientemente cercana al cero deseado. Sin embargo, cabe destacar que este método puede presentar algunas limitaciones, como la convergencia a mínimos locales o puntos en los que la derivada se anule.

Cómo se pueden utilizar los ceros calculados en MATLAB para diseñar filtros o sistemas de control

Los ceros calculados en MATLAB son una herramienta invaluable para el diseño de filtros o sistemas de control. Estos ceros representan los valores de frecuencia en los cuales la respuesta del sistema es cero, lo que implica que no hay amplificación o atenuación en esa frecuencia específica.

Al conocer los ceros de un sistema, podemos utilizar esta información para diseñar filtros personalizados o sistemas de control que cumplan con nuestros requisitos específicos. Por ejemplo, si deseamos enfatizar ciertas frecuencias en la salida de un sistema, podemos colocar ceros en esas frecuencias para lograr la amplificación deseada.

Además, los ceros pueden ayudarnos a mejorar la estabilidad de un sistema. Al colocar ceros en ciertas frecuencias, podemos compensar los efectos indeseables de los polos y lograr un mejor comportamiento del sistema.

Los ceros calculados en MATLAB nos brindan la capacidad de diseñar filtros y sistemas de control de manera más precisa y personalizada. Al aprovechar esta herramienta, podemos lograr respuestas de frecuencia específicas y mejorar la estabilidad de nuestros sistemas.

Preguntas frecuentes (FAQ)

1. ¿Qué es un polo en MATLAB?

Un polo en MATLAB es una raíz del denominador de una función de transferencia, que representa una frecuencia en la cual la respuesta del sistema se vuelve infinita.

2. ¿Qué es un cero en MATLAB?

Un cero en MATLAB es una raíz del numerador de una función de transferencia, que representa una frecuencia en la cual la respuesta del sistema se anula o se hace cero.

3. ¿Cómo puedo encontrar los ceros de una función de transferencia en MATLAB?

En MATLAB, puedes utilizar la función zero para encontrar los ceros de una función de transferencia. Simplemente ingresa la función de transferencia como argumento y MATLAB te devolverá los ceros.

4. ¿Puedo encontrar los ceros de una función de transferencia con polos complejos en MATLAB?

Sí, en MATLAB también puedes encontrar los ceros de una función de transferencia con polos complejos. La función zero te mostrará los ceros complejos y conjugados correspondientes.

5. ¿Qué puedo hacer con los ceros de una función de transferencia en MATLAB?

Los ceros de una función de transferencia en MATLAB te permiten analizar y comprender el comportamiento del sistema. Puedes utilizarlos para determinar la estabilidad, la respuesta en frecuencia y otras características del sistema.