
Calcula la anchura a media altura en MATLAB: métodos y ejemplos
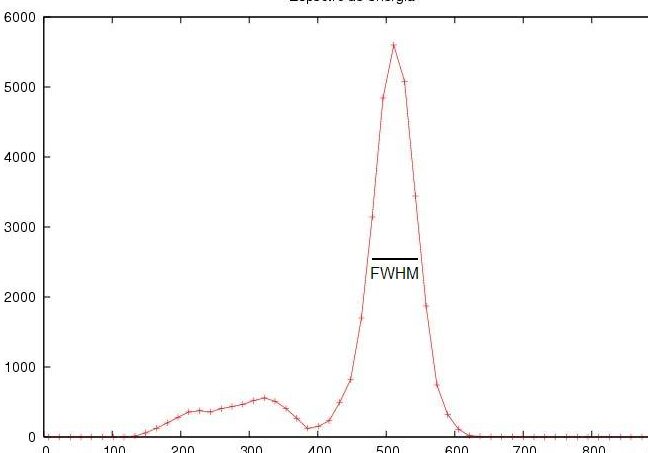
En el campo de la ciencia y la ingeniería, es común encontrarnos con la necesidad de calcular la anchura a media altura (FWHM, por sus siglas en inglés) de una señal. Este parámetro es importante para caracterizar la resolución de un sistema de medición y es especialmente utilizado en espectroscopia, análisis de señales y procesamiento de imágenes.
Exploraremos los métodos y técnicas para calcular la anchura a media altura en MATLAB, un popular software de programación utilizado en la comunidad científica. Analizaremos desde los métodos básicos hasta aquellos más avanzados, e ilustraremos cada uno de ellos con ejemplos prácticos. Si estás interesado en aprender a calcular la FWHM utilizando MATLAB, ¡sigue leyendo!
- Cuál es la importancia de calcular la anchura a media altura en el análisis de datos en MATLAB
- Cuáles son los métodos más utilizados para calcular la anchura a media altura en MATLAB
- Cómo se puede implementar el método de interpolación para calcular la anchura a media altura en MATLAB
- Existen funciones predefinidas en MATLAB que facilitan el cálculo de la anchura a media altura
- Qué ejemplos prácticos se pueden utilizar para entender mejor el cálculo de la anchura a media altura en MATLAB
- Cuáles son las limitaciones o consideraciones importantes al calcular la anchura a media altura en MATLAB
- Cuál es la relación entre la anchura a media altura y otros parámetros de interés en el análisis de datos en MATLAB
- Qué recomendaciones o mejores prácticas se pueden seguir al calcular la anchura a media altura en MATLAB
- Cuáles son las ventajas y desventajas de utilizar MATLAB para el cálculo de la anchura a media altura en comparación con otros programas o lenguajes de programación
- Dónde se puede encontrar más información o recursos para aprender más sobre el cálculo de la anchura a media altura en MATLAB
-
Preguntas frecuentes (FAQ)
- ¿Qué es la anchura a media altura?
- ¿Por qué es importante calcular la anchura a media altura?
- ¿Cuáles son los métodos más utilizados para calcular la anchura a media altura en MATLAB?
- ¿Cómo puedo calcular la anchura a media altura en MATLAB?
- ¿Puedes darme un ejemplo de cómo calcular la anchura a media altura en MATLAB?
Cuál es la importancia de calcular la anchura a media altura en el análisis de datos en MATLAB
La anchura a media altura es una medida importante en el análisis de datos, especialmente en MATLAB. Este cálculo se utiliza para determinar la dispersión de los datos alrededor de un punto central. Es comúnmente utilizado en diversas disciplinas científicas y técnicas, como la física, química, bioinformática y procesamiento de señales.
En MATLAB, existen varios métodos para calcular la anchura a media altura, cada uno con sus ventajas y desventajas. Estos métodos incluyen la estimación de la anchura utilizando funciones predefinidas, el ajuste de curva y la interpolación.
Calcular la anchura a media altura es esencial para comprender y analizar datos de manera más precisa. Permite identificar patrones y tendencias, y también proporciona información sobre la calidad y confiabilidad de los datos.
A continuación, se presentan algunos ejemplos prácticos para ilustrar cómo calcular la anchura a media altura en MATLAB utilizando diferentes métodos y funciones en el lenguaje de programación.
Cuáles son los métodos más utilizados para calcular la anchura a media altura en MATLAB
La anchura a media altura es una medida comúnmente utilizada en el procesamiento de señales y análisis de datos en MATLAB. Existen varios métodos que permiten calcular esta medida, cada uno con sus ventajas y desventajas.
Método del umbral
Este método consiste en establecer un umbral a partir del cual se considerará que la señal alcanza la media altura. A partir de este umbral, se calcula la anchura como la distancia entre los puntos en los que la señal cruza el umbral.
Método de la curva ajustada
En este método, se ajusta una curva a la señal y se determinan los puntos en los que la curva alcanza la media altura. Luego, se calcula la anchura como la distancia entre estos puntos.
Método de interpolación
Este método utiliza técnicas de interpolación para determinar los puntos en los que la señal alcanza la media altura. A partir de estos puntos, se calcula la anchura de la misma manera que en los métodos anteriores.
Ejemplos de implementación en MATLAB
A continuación, se presentarán ejemplos de cómo implementar estos métodos en MATLAB:
% Método del umbral
umbral = mean(signal) / 2;
indices_cruce = find(signal > umbral);
anchura_umbral = indices_cruce(end) - indices_cruce(1);
% Método de la curva ajustada
curva_ajustada = fit(x, signal, 'gauss1');
altura_media = curva_ajustada.a1 / 2;
indices_cruce = find(curva_ajustada(x) > altura_media);
anchura_curva = x(indices_cruce(end)) - x(indices_cruce(1));
% Método de interpolación
altura_media = mean(signal) / 2;
indices_cruce = find(interp1(x, signal, altura_media, 'linear') > altura_media);
anchura_interpolacion = x(indices_cruce(end)) - x(indices_cruce(1));
Estos son solo algunos ejemplos de cómo calcular la anchura a media altura en MATLAB. Dependiendo de las características de la señal y del análisis que se requiera, puede ser necesario adaptar o combinar estos métodos para obtener resultados precisos y confiables.
Cómo se puede implementar el método de interpolación para calcular la anchura a media altura en MATLAB
En MATLAB, el método de interpolación se puede utilizar para calcular la anchura a media altura de una señal. Este método consiste en encontrar los puntos donde la señal alcanza el 50% de su valor máximo y luego interpolar entre estos puntos para obtener el ancho a media altura.
Para implementar este método en MATLAB, primero necesitamos cargar la señal y encontrar su valor máximo. Luego, calculamos el valor del 50% del máximo y encontramos los puntos donde la señal alcanza este valor utilizando la función "find". Estos puntos corresponden a los límites de la anchura a media altura.
A continuación, utilizamos la función "interp1" para interpolar entre estos puntos y obtener la posición exacta donde la señal alcanza el 50% de su valor máximo. Finalmente, calculamos la anchura a media altura como la diferencia entre estas posiciones.
Ejemplo de implementación del método de interpolación en MATLAB
% Cargar la señal
load('signal.mat');
% Encontrar el valor máximo
max_value = max(signal);
% Calcular el valor del 50% del máximo
half_value = 0.5 max_value;
% Encontrar los puntos donde la señal alcanza el 50% del máximo
indices = find(signal >= half_value);
% Interpolar entre estos puntos
interpolated_points = interp1(signal(indices), indices, half_value);
% Calcular la anchura a media altura
width = diff(interpolated_points);
Este ejemplo ilustra cómo implementar el método de interpolación en MATLAB para calcular la anchura a media altura de una señal. Sin embargo, es importante tener en cuenta que este método puede no ser adecuado para todas las señales y puede requerir ajustes adicionales dependiendo de la naturaleza de la señal.
Existen funciones predefinidas en MATLAB que facilitan el cálculo de la anchura a media altura
Una de estas funciones es la función "findpeaks", que permite encontrar los picos en un conjunto de datos. Para calcular la anchura a media altura, primero se deben encontrar los máximos locales del conjunto de datos. Luego, se puede utilizar la función "halfwidth" para calcular la anchura a media altura de cada pico.
Otra función útil es "interp1", que permite interpolar los datos para obtener una resolución más fina. Esto es especialmente útil si los datos tienen una resolución baja y se necesita una mayor precisión en el cálculo de la anchura a media altura.
Además de estas funciones predefinidas, también es posible implementar métodos propios para calcular la anchura a media altura en MATLAB. Por ejemplo, se puede utilizar la técnica de interpolación lineal para encontrar los puntos en la curva que tienen un valor igual a la mitad de la altura del pico. Luego, se puede calcular la distancia entre estos puntos para obtener la anchura a media altura.
Ejemplo de cálculo de la anchura a media altura en MATLAB
Supongamos que tenemos un conjunto de datos almacenado en el vector "x" y queremos calcular la anchura a media altura de los picos. Podemos utilizar la siguiente secuencia de comandos:
= findpeaks(x);
Esta línea de código encuentra los picos en el vector "x" y devuelve los valores de los picos en el vector "pks" y las ubicaciones de los picos en el vector "locs".
hw = halfwidth(x,locs);
Esta línea de código utiliza la función "halfwidth" para calcular la anchura a media altura de cada pico en el vector "x" utilizando las ubicaciones de los picos en el vector "locs". El resultado se almacena en el vector "hw".
Después de ejecutar estas líneas de código, tendremos la anchura a media altura de cada pico en el vector "hw". Podemos utilizar esta información para analizar y comparar los picos en nuestro conjunto de datos.
Qué ejemplos prácticos se pueden utilizar para entender mejor el cálculo de la anchura a media altura en MATLAB
El cálculo de la anchura a media altura es una técnica comúnmente utilizada en el procesamiento de señales y la espectroscopia para determinar la resolución de un pico o una banda de frecuencia. MATLAB, siendo un lenguaje de programación ampliamente utilizado en el análisis de datos, proporciona diversas herramientas para llevar a cabo este cálculo de manera eficiente y precisa.
Para entender mejor el cálculo de la anchura a media altura en MATLAB, es útil considerar algunos ejemplos prácticos. Estos ejemplos nos permitirán visualizar cómo se realiza el cálculo y cómo se pueden utilizar las diversas funciones y herramientas disponibles en MATLAB para obtener resultados precisos.
Ejemplo 1: Cálculo de la anchura a media altura de un pico en una señal
Imaginemos que tenemos una señal de audio y queremos determinar la anchura a media altura del pico correspondiente a una cierta frecuencia. En MATLAB, podemos utilizar la función de transformada rápida de Fourier (FFT) para obtener el espectro de frecuencia de la señal. A continuación, podemos encontrar el pico correspondiente a la frecuencia de interés y calcular su anchura a media altura utilizando una combinación de técnicas de interpolación y análisis de amplitud.
Una vez que hemos calculado la anchura a media altura del pico, podemos utilizar esta información para evaluar la resolución de nuestro sistema de detección de frecuencia. Esto es especialmente útil en aplicaciones de audio donde la capacidad de distinguir frecuencias cercanas es fundamental.
Ejemplo 2: Cálculo de la anchura a media altura de una banda de frecuencia en un espectro
Otro ejemplo práctico que ilustra el cálculo de la anchura a media altura en MATLAB es el análisis de un espectro de frecuencia. Supongamos que tenemos un espectro de frecuencia que representa la respuesta de un sistema a diferentes frecuencias de entrada. Queremos determinar la anchura a media altura de una banda de frecuencia específica para evaluar la selectividad del sistema.
En este caso, podemos utilizar técnicas de filtrado y análisis de amplitud en MATLAB para identificar los límites de la banda de frecuencia y calcular su anchura a media altura. Esto nos permitirá evaluar la capacidad del sistema para discriminar entre diferentes frecuencias y determinar su capacidad de selectividad.
El cálculo de la anchura a media altura en MATLAB es una herramienta fundamental en el análisis de señales y espectroscopia. A través de diversos ejemplos prácticos, hemos demostrado cómo utilizar las funciones y herramientas disponibles en MATLAB para realizar este cálculo de manera precisa y eficiente. Ya sea analizando picos individuales en una señal o bandas de frecuencia en un espectro, MATLAB ofrece las capacidades necesarias para realizar estos cálculos con facilidad.
Cuáles son las limitaciones o consideraciones importantes al calcular la anchura a media altura en MATLAB
Al calcular la anchura a media altura en MATLAB, es importante tener en cuenta algunas limitaciones y consideraciones importantes. En primer lugar, debemos asegurarnos de que los datos de entrada sean suficientemente suaves y continuos. Si los datos contienen ruido o fluctuaciones significativas, el cálculo de la anchura a media altura puede no ser válido.
Otra consideración importante es el método utilizado para calcular la anchura a media altura. Existen diferentes métodos disponibles en MATLAB, como el método de interpolación o el uso de ajustes de curvas. Es importante seleccionar el método adecuado según las características de los datos y los requisitos del problema.
Además, es importante recordar que el cálculo de la anchura a media altura es sensible a los parámetros de umbral utilizados. Pequeños cambios en el umbral pueden tener un impacto significativo en los resultados. Por lo tanto, es necesario seleccionar cuidadosamente los valores de umbral para obtener resultados precisos y consistentes.
Por último, es importante considerar el rendimiento computacional al calcular la anchura a media altura en MATLAB. Dependiendo del tamaño de los datos y la complejidad del cálculo, puede ser necesario optimizar el código o utilizar técnicas de paralelización para acelerar el proceso.
Cuál es la relación entre la anchura a media altura y otros parámetros de interés en el análisis de datos en MATLAB
La anchura a media altura es un parámetro importante en el análisis de datos en MATLAB, ya que puede proporcionar información valiosa sobre la forma de una señal o distribución de datos. Esta medida representa la distancia entre los puntos donde la señal o distribución alcanza la mitad del máximo valor.
La anchura a media altura puede estar relacionada con otros parámetros de interés, como la frecuencia central de una señal o el valor medio de una distribución. Por ejemplo, si la anchura a media altura es grande, esto puede indicar que la señal o distribución es amplia o dispersa, mientras que una anchura a media altura pequeña puede indicar una señal o distribución estrecha o concentrada.
Para calcular la anchura a media altura en MATLAB, existen varios métodos disponibles. Estos métodos incluyen el método de interpolación, el método de ajuste de curva y el método de búsqueda de puntos de inflexión. Cada método tiene sus propias ventajas y desventajas, y la elección del método adecuado dependerá del tipo de datos y del análisis que se esté realizando.
Método de interpolación
El método de interpolación es uno de los métodos más utilizados para calcular la anchura a media altura en MATLAB. Este método consiste en interpolar la señal o distribución para encontrar los puntos donde alcanza la mitad del máximo valor. Una vez que se han encontrado estos puntos, se calcula la distancia entre ellos para obtener la anchura a media altura.
Existen diferentes tipos de interpolación que se pueden utilizar, como la interpolación lineal, la interpolación polinómica y la interpolación spline. Cada tipo de interpolación tiene sus propias características y puede ser más adecuado para diferentes situaciones. Por ejemplo, la interpolación lineal es rápida y sencilla, pero puede no ser adecuada para señales o distribuciones con formas complejas.
Método de ajuste de curva
Otro método comúnmente utilizado para calcular la anchura a media altura en MATLAB es el método de ajuste de curva. Este método consiste en ajustar una función o curva a la señal o distribución y luego encontrar los puntos donde la función alcanza la mitad del máximo valor. Una vez que se han encontrado estos puntos, se calcula la distancia entre ellos para obtener la anchura a media altura.
Existen diferentes tipos de funciones o curvas que se pueden ajustar, como polinomios, funciones trigonométricas y funciones exponenciales. La elección de la función adecuada dependerá del tipo de datos y del análisis que se esté realizando. Por ejemplo, si la señal tiene una forma sinusoidal, puede ser más adecuado ajustar una función trigonométrica.
Método de búsqueda de puntos de inflexión
El método de búsqueda de puntos de inflexión es otro enfoque utilizado para calcular la anchura a media altura en MATLAB. Este método consiste en encontrar los puntos donde se produce un cambio en la concavidad de la señal o distribución, es decir, donde la segunda derivada cambia de signo. Estos puntos corresponden a los puntos donde la señal o distribución alcanza la mitad del máximo valor.
El método de búsqueda de puntos de inflexión puede ser útil cuando se trabaja con señales o distribuciones que no se pueden interpolar o ajustar fácilmente. Sin embargo, este método puede ser más complejo y requiere un mayor esfuerzo computacional que los otros métodos mencionados anteriormente.
Ejemplos de cálculo de anchura a media altura en MATLAB
A continuación, se presentan algunos ejemplos de cómo calcular la anchura a media altura en MATLAB utilizando los métodos mencionados anteriormente.
Ejemplo 1: Calcular la anchura a media altura de una señal sinusoidal utilizando el método de interpolación:
% Generar señal sinusoidal
t = 0:0.001:1;
f = 10;
x = sin(2pift);
% Interpolar señal
xi = interp1(x, t, max(x)/2);
% Calcular anchura a media altura
amplitude = max(x)-min(x);
half_width = xi(2) - xi(1);
Ejemplo 2: Calcular la anchura a media altura de una distribución de datos utilizando el método de ajuste de curva:
% Generar distribución de datos
data = randn(1000,1);
% Ajustar curva a distribución
curve = fitdist(data,'Normal');
% Encontrar puntos de media altura
half_value = curve.mean - curve.sigma/2;
xi = icdf(curve, );
% Calcular anchura a media altura
half_width = xi(2) - xi(1);
Ejemplo 3: Calcular la anchura a media altura de una señal utilizando el método de búsqueda de puntos de inflexión:
% Generar señal
t = 0:0.001:1;
f = 10;
x = sin(2pift);
% Calcular segunda derivada de la señal
d2x = diff(diff(x));
% Encontrar puntos de inflexión
inflexion_points = find(d2x<0);
% Encontrar puntos de media altura
half_value = max(x)/2;
xi = ;
for i = 1:length(inflexion_points)
if x(inflexion_points(i)) < half_value && x(inflexion_points(i)+1) > half_value
xi = , , half_value)];
elseif x(inflexion_points(i)) > half_value && x(inflexion_points(i)+1) < half_value
xi = , , half_value)];
end
end
% Calcular anchura a media altura
half_width = xi(2) - xi(1);
Qué recomendaciones o mejores prácticas se pueden seguir al calcular la anchura a media altura en MATLAB
Al calcular la anchura a media altura en MATLAB, es importante seguir algunas recomendaciones y mejores prácticas para obtener resultados precisos y confiables.
1. Preprocesamiento de datos: Antes de realizar cualquier cálculo, es fundamental preprocesar los datos. Esto implica eliminar cualquier ruido o artefacto, suavizar la señal si es necesario y asegurarse de que los datos estén en el formato adecuado para el análisis.
2. Selección adecuada del algoritmo: Existen varios métodos para calcular la anchura a media altura en MATLAB, como el método de interpolación, el método de ajuste de curvas o el método de convolución. Es importante seleccionar el método más adecuado para los datos y el propósito del análisis.
3. Validación y verificación: Antes de utilizar los resultados del cálculo, es crucial validar y verificar la precisión de los mismos. Esto puede implicar comparar los resultados con métodos alternativos, establecer criterios de aceptación y realizar pruebas de sensibilidad.
4. Documentación y reproducibilidad: Es recomendable documentar todos los pasos realizados en el cálculo, incluyendo los parámetros utilizados, los métodos seleccionados y cualquier consideración especial. Esto permitirá reproducir los resultados en el futuro y facilitar la colaboración con otros investigadores.
Al calcular la anchura a media altura en MATLAB, es importante preprocesar los datos, seleccionar el algoritmo adecuado, validar los resultados y documentar todos los pasos realizados. Siguiendo estas recomendaciones, se pueden obtener resultados precisos y reproducibles.
Cuáles son las ventajas y desventajas de utilizar MATLAB para el cálculo de la anchura a media altura en comparación con otros programas o lenguajes de programación
Existen varias ventajas y desventajas al utilizar MATLAB para el cálculo de la anchura a media altura en comparación con otros programas o lenguajes de programación.
Una de las ventajas de MATLAB es su facilidad de uso y su amplia gama de funciones y herramientas para el análisis de datos. Esto hace que sea más sencillo y eficiente realizar el cálculo de la anchura a media altura en MATLAB en comparación con otros programas.
Otra ventaja de MATLAB es su capacidad para manejar grandes conjuntos de datos y realizar cálculos complejos de manera rápida. Esto es especialmente útil cuando se trabaja con señales o imágenes que contienen una gran cantidad de datos.
Sin embargo, también hay algunas desventajas en el uso de MATLAB para el cálculo de la anchura a media altura. Una de ellas es que MATLAB es un software propietario y puede ser costoso adquirir una licencia. Esto puede limitar su acceso para aquellos con presupuestos limitados.
Además, aunque MATLAB es un lenguaje de programación muy poderoso, puede tener una curva de aprendizaje pronunciada para aquellos que no están familiarizados con él. Esto puede requerir tiempo adicional para aprender y dominar el lenguaje antes de poder utilizarlo eficientemente en el cálculo de la anchura a media altura.
Por otro lado, existen otros programas y lenguajes de programación que también pueden ser utilizados para el cálculo de la anchura a media altura, como Python o R. Estos lenguajes son de código abierto y gratuitos, lo que los hace más accesibles para aquellos con presupuestos limitados.
El uso de MATLAB para el cálculo de la anchura a media altura tiene varias ventajas, como su facilidad de uso y eficiencia en el manejo de grandes conjuntos de datos. Sin embargo, también hay desventajas, como su costo y su curva de aprendizaje pronunciada. Es importante considerar estas ventajas y desventajas al decidir qué programa o lenguaje utilizar para el cálculo de la anchura a media altura.
Dónde se puede encontrar más información o recursos para aprender más sobre el cálculo de la anchura a media altura en MATLAB
Si estás interesado en aprender más sobre el cálculo de la anchura a media altura en MATLAB, existen varios recursos disponibles que puedes utilizar para ampliar tus conocimientos.
Una excelente opción es buscar tutoriales en línea. Hay muchos sitios web que ofrecen tutoriales gratuitos o de pago que te guían paso a paso en el cálculo de la anchura a media altura utilizando MATLAB. Estos tutoriales suelen incluir ejemplos prácticos y ejercicios para que puedas practicar tus habilidades.
Otra opción es revisar la documentación oficial de MATLAB. MATLAB proporciona una amplia documentación en línea que cubre diferentes aspectos de la programación, incluido el cálculo de la anchura a media altura. En la documentación, encontrarás ejemplos de código, explicaciones detalladas y referencias a funciones específicas que puedes utilizar en tu proyecto.
Además de los tutoriales y la documentación oficial, también puedes buscar libros especializados en MATLAB y el cálculo numérico. Los libros pueden brindarte una comprensión más profunda y te permitirán explorar diferentes enfoques y técnicas utilizadas en el cálculo de la anchura a media altura en MATLAB. Algunos libros incluso pueden incluir ejemplos de código y ejercicios prácticos para que puedas aplicar lo que has aprendido.
Por último, no olvides aprovechar la comunidad en línea de MATLAB. Hay muchos foros y grupos de discusión donde puedes hacer preguntas, compartir tus experiencias y aprender de otros usuarios de MATLAB que también están interesados en el cálculo de la anchura a media altura. Participar en estos grupos te brindará la oportunidad de obtener ayuda y consejos de expertos en el campo.
Si quieres aprender más sobre el cálculo de la anchura a media altura en MATLAB, existen varias fuentes de información disponibles. Puedes utilizar tutoriales en línea, la documentación oficial de MATLAB, libros especializados y la comunidad en línea para ampliar tu conocimiento y mejorar tus habilidades en este campo.
Preguntas frecuentes (FAQ)
¿Qué es la anchura a media altura?
La anchura a media altura es un parámetro utilizado para cuantificar la dispersión de una señal. Representa la distancia entre los puntos en los que la señal alcanza el 50% de su valor máximo.
¿Por qué es importante calcular la anchura a media altura?
Calcular la anchura a media altura es importante en diversos campos como la física, la ingeniería y la biomedicina. Permite determinar la resolución de una señal, identificar picos de interés y cuantificar la variabilidad de un experimento.
¿Cuáles son los métodos más utilizados para calcular la anchura a media altura en MATLAB?
En MATLAB, los métodos más utilizados para calcular la anchura a media altura son el método del máximo y el método de interpolación. Estos métodos permiten obtener una estimación precisa de la anchura a media altura.
¿Cómo puedo calcular la anchura a media altura en MATLAB?
Para calcular la anchura a media altura en MATLAB, puedes utilizar las funciones built-in como "findpeaks" y "interp1", que te facilitan la búsqueda de los puntos de interés y la interpolación entre ellos.
¿Puedes darme un ejemplo de cómo calcular la anchura a media altura en MATLAB?
Sí, por supuesto. A continuación te muestro un ejemplo de cómo calcular la anchura a media altura de una señal utilizando el método del máximo en MATLAB:
```matlab
% Definir la señal
x = linspace(0, 10, 100);
y = sin(x);
% Encontrar el máximo de la señal
= max(y);
% Calcular los puntos a media altura
half_height = max_value / 2;
left_point = interp1(y(1:max_index), x(1:max_index), half_height);
right_point = interp1(y(max_index:end), x(max_index:end), half_height);
% Calcular la anchura a media altura
width = right_point - left_point;
% Mostrar el resultado
disp();
```
Este código calculará la anchura a media altura de la señal senoidal en el intervalo .
Deja una respuesta








Artículos que podrían interesarte