Calcula fácilmente los polos y ceros en Matlab: guía completa

Matlab es un lenguaje de programación ampliamente utilizado en campos como la ingeniería, la física y las matemáticas. Una de las características más poderosas que ofrece es su capacidad para analizar y manipular sistemas de ecuaciones y funciones. En particular, Matlab facilita el cálculo de los polos y ceros de una función, lo cual es fundamental para comprender el comportamiento de un sistema. Exploraremos cómo utilizar Matlab para calcular fácilmente los polos y ceros de una función.

En las siguientes secciones, te guiaré paso a paso a través del proceso de calcular los polos y ceros en Matlab. Empezaremos por entender qué son los polos y ceros y por qué son importantes en el análisis de sistemas. Luego, veremos cómo representar una función en Matlab y cómo utilizar las funciones incorporadas para encontrar los polos y ceros. También exploraremos algunos ejemplos prácticos para ilustrar mejor el proceso. Al final del artículo, tendrás todas las herramientas necesarias para realizar cálculos de polos y ceros en Matlab de manera eficiente y precisa.

Qué son los polos y ceros en el contexto de Matlab

En el contexto de Matlab, los polos y ceros son conceptos fundamentales en el análisis y diseño de sistemas. Los polos representan las ubicaciones en el plano complejo donde la función de transferencia del sistema se anula, mientras que los ceros corresponden a las ubicaciones donde la función de transferencia se vuelve cero.

Estos polos y ceros son esenciales para comprender y caracterizar el comportamiento de un sistema en términos de estabilidad, respuesta transitoria y respuesta en frecuencia. Además, también desempeñan un papel crucial en aplicaciones como el control de sistemas y el filtrado de señales.

En Matlab, el análisis de polos y ceros se puede realizar utilizando diversas herramientas y funciones que facilitan su cálculo y representación gráfica. En esta guía completa, aprenderemos cómo calcular y visualizar los polos y ceros de diferentes sistemas utilizando las capacidades de Matlab.

Cómo afectan los polos y ceros al comportamiento de un sistema en Matlab

Los polos y ceros son conceptos fundamentales en el análisis de sistemas en Matlab. Los polos son las raíces del denominador de la función de transferencia del sistema, mientras que los ceros son las raíces del numerador. Estos elementos determinan las características y el comportamiento del sistema.

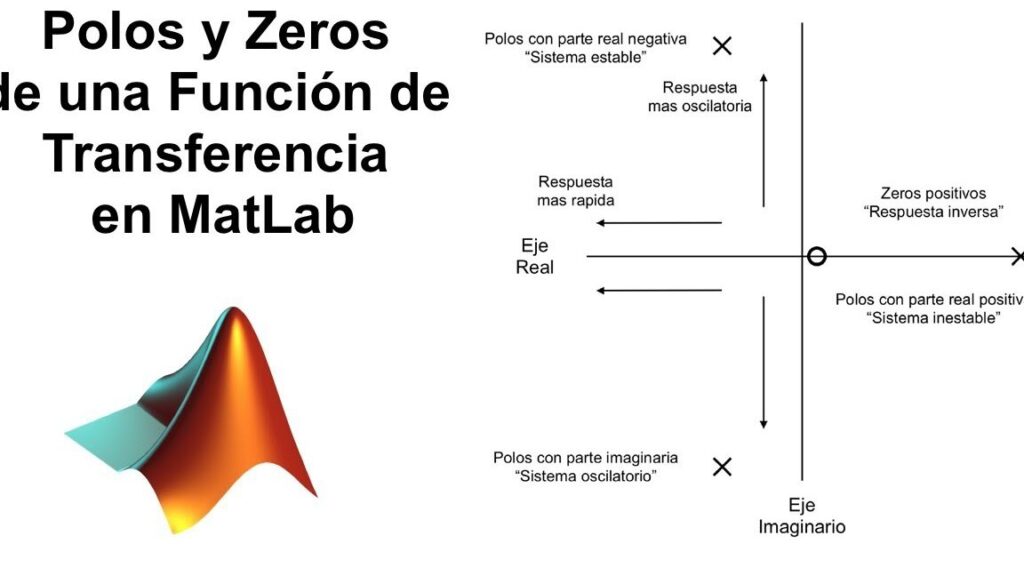
Los polos pueden ser reales o complejos, y su ubicación en el plano complejo afecta la estabilidad y la respuesta del sistema. Si los polos se encuentran en el semiplano derecho, el sistema será inestable. Por otro lado, los ceros pueden cancelar los polos y mejorar la respuesta del sistema en términos de atenuación de ciertas frecuencias o aumentar la ganancia.

En Matlab, calcular los polos y ceros de un sistema es muy sencillo. Puedes utilizar la función tf para crear la función de transferencia y luego utilizar las funciones pole y zero para obtener los polos y ceros respectivamente.

Para ilustrar esto, consideremos un sistema de segundo orden con una función de transferencia H(s) = 1/((s+2)(s+3)). Podemos crear esta función utilizando la siguiente línea de código:

H = tf(, )

Una vez que tenemos la función de transferencia, podemos utilizar las funciones pole y zero para calcular los polos y ceros:

p = pole(H)
z = zero(H)

En este caso, obtendríamos p = y z = , lo que indica que el sistema tiene dos polos reales en -2 y -3, y ningún cero.

Conociendo los polos y ceros de un sistema, podemos analizar su respuesta en el dominio del tiempo mediante la función impulse o la función step, o en el dominio de la frecuencia utilizando la función bode o la función nyquist.

Los polos y ceros son elementos clave para comprender el comportamiento de un sistema en Matlab. Con las funciones adecuadas, podemos calcular fácilmente estos parámetros y utilizarlos para analizar y diseñar sistemas de control o procesamiento de señales.

Cuál es la importancia de calcular los polos y ceros en Matlab

El cálculo de los polos y ceros en Matlab es una herramienta esencial para el análisis de sistemas dinámicos. Los polos y ceros son puntos importantes en el plano complejo que determinan el comportamiento del sistema, como su estabilidad y respuesta en frecuencia.

Conocer los polos y ceros de un sistema permite identificar la influencia de cada componente en la respuesta total del sistema. Esto es crucial para el diseño y optimización de sistemas de control, comunicaciones, procesamiento de señales y muchas otras aplicaciones.

En Matlab, el cálculo de polos y ceros se puede realizar de manera rápida y sencilla utilizando funciones específicas. Con esta guía completa, aprenderás paso a paso cómo realizar estas operaciones y cómo interpretar los resultados obtenidos.

Cuáles son las distintas formas de representar los polos y ceros en Matlab

Existen varias formas de representar los polos y ceros en Matlab. Una forma común es a través de la función tf(), que representa una función de transferencia en términos de polos y ceros. Por ejemplo, podemos definir una función de transferencia y luego utilizar la función tf2zpk() para obtener los polos y ceros correspondientes.

Otra forma de representar los polos y ceros es a través de la función zpk(), que toma como argumentos los polos y ceros y devuelve la función de transferencia correspondiente. También podemos utilizar la función pzmap() para graficar los polos y ceros en el plano complejo.

Además, podemos utilizar la función roots() para calcular los polos y ceros de un polinomio dado. Esta función devuelve los valores de los polos y ceros en forma de matriz.

Existen varias formas de representar los polos y ceros en Matlab, ya sea a través de funciones específicas como tf() y zpk(), o utilizando funciones más generales como pzmap() y roots(). Estas herramientas nos permiten calcular y visualizar de manera fácil los polos y ceros en Matlab.

Cuáles son las técnicas más utilizadas para calcular los polos y ceros en Matlab

Calcular los polos y ceros en Matlab es una tarea común para los ingenieros y científicos que trabajan con sistemas dinámicos. Afortunadamente, Matlab ofrece diversas técnicas y herramientas para facilitar este proceso.

Una de las técnicas más utilizadas es la función tf2zp, que convierte una función de transferencia en sus polos y ceros correspondientes. Esta función es especialmente útil cuando se trabaja con sistemas lineales y se conoce la función de transferencia exacta.

Otra técnica común es la utilización de la función tf, que permite crear una función de transferencia utilizando coeficientes de polinomios. Una vez definida la función de transferencia, se pueden utilizar las funciones roots y pole para obtener los ceros y polos respectivamente.

Si se dispone de datos en forma de respuesta temporal, se puede emplear la función tfestimate para estimar la función de transferencia y posteriormente obtener los polos y ceros utilizando las técnicas mencionadas anteriormente.

Matlab ofrece diferentes métodos para calcular los polos y ceros de una función de transferencia o sistema dinámico. Estas técnicas facilitan el análisis y diseño de sistemas, permitiendo a los ingenieros y científicos obtener información valiosa sobre el comportamiento de los sistemas.

Existen métodos automáticos para calcular los polos y ceros en Matlab

La determinación de los polos y ceros es una parte fundamental en el análisis de sistemas lineales en Matlab. Afortunadamente, existen métodos automáticos que facilitan este proceso y permiten obtener resultados precisos de manera rápida y eficiente.

Uno de los métodos más utilizados es la función tf2zp, la cual permite convertir una función de transferencia en sus polos y ceros correspondientes. Esta función toma como argumentos de entrada los coeficientes del numerador y el denominador de la función de transferencia y devuelve una matriz con los polos y otra con los ceros.

Además de la función tf2zp, Matlab cuenta con otras herramientas poderosas para calcular los polos y ceros, como la función tfdata, que retorna los coeficientes numéricos de la función de transferencia en una matriz, lo cual facilita su manipulación y análisis.

Otro enfoque común es utilizar el comando roots, el cual permite calcular los polos de un polinomio en forma de vector. Este comando devuelve los valores de los polos en una matriz y es especialmente útil cuando se trabaja con polinomios de alta orden.

Para facilitar aún más el cálculo de los polos y ceros, Matlab proporciona la función polystab, la cual permite estabilizar un sistema lineal inestable a través de la técnica de descomposición en fracciones parciales.

Matlab ofrece diversas herramientas y funciones que facilitan el cálculo de los polos y ceros en sistemas lineales. Estas herramientas automáticas agilizan el proceso y brindan resultados precisos, lo que hace que el análisis y diseño de sistemas sea más eficiente y accesible para los usuarios de Matlab.

Cuál es la sintaxis básica para calcular los polos y ceros en Matlab

En Matlab, calcular los polos y ceros de un sistema es fundamental para comprender sus características y comportamiento. La sintaxis básica para realizar esta tarea es muy sencilla.

Para calcular los polos de un sistema en Matlab, se utiliza la función pole(sys), donde sys es el sistema dado en forma de función de transferencia, estado o espacio de estados. Esta función devolverá un vector con los valores de los polos del sistema.

Por otro lado, para calcular los ceros de un sistema en Matlab, se utiliza la función zero(sys). Al igual que en el caso anterior, sys representa el sistema en forma de función de transferencia, estado o espacio de estados. La función zero(sys) devolverá un vector con los valores de los ceros del sistema.

Es importante destacar que tanto la función pole como la función zero son aplicables a diferentes tipos de sistemas en Matlab, como sistemas de tiempo continuo o sistemas de tiempo discreto.

Una vez que hemos calculado los polos y ceros de un sistema en Matlab, podemos utilizar esta información para analizar su estabilidad, respuesta en frecuencia, entre otros aspectos importantes en el diseño y análisis de sistemas.

Cuáles son los parámetros que se deben tener en cuenta al calcular los polos y ceros en Matlab

Al calcular los polos y ceros en Matlab, hay varios parámetros importantes que debemos considerar. En primer lugar, necesitamos tener en cuenta la función de transferencia del sistema, que puede ser representada como un cociente polinómico.

Además, debemos establecer los valores de las variables que componen dicha función de transferencia, como los coeficientes de los polinomios numerador y denominador, y los valores de las variables independientes si la función de transferencia es dependiente del tiempo.

Por otro lado, también es relevante definir si queremos calcular los polos y ceros en tiempo continuo o tiempo discreto. Esto influirá en la forma en que interpretamos los resultados y cómo aplicamos los métodos de cálculo.

Los parámetros clave para calcular los polos y ceros en Matlab son la función de transferencia, los valores de las variables y la elección entre tiempo continuo o tiempo discreto.

Cuáles son las limitaciones o posibles errores al calcular los polos y ceros en Matlab

Cuando se trata de calcular polos y ceros en Matlab, es importante tener en cuenta algunas limitaciones y posibles errores que pueden surgir durante el proceso.

Uno de los posibles problemas que puede surgir es la presencia de polos o ceros múltiples. En estos casos, es posible que Matlab no pueda calcularlos correctamente y se obtengan resultados incorrectos.

Otro aspecto a considerar es la precisión numérica. Matlab utiliza una representación finita de números reales, lo que puede llevar a errores de redondeo al calcular polos y ceros. Es recomendable establecer una tolerancia adecuada para reducir estos errores.

También es importante tener en cuenta que Matlab puede presentar problemas al calcular polos y ceros en sistemas de gran tamaño. En estos casos, puede ser necesario utilizar herramientas adicionales para obtener resultados precisos.

Además, es fundamental verificar que los datos de entrada sean correctos y estén en el formato adecuado. Errores en la entrada de datos pueden llevar a resultados incorrectos o inesperados al calcular polos y ceros en Matlab.

También es importante considerar el efecto de la calidad de la señal de entrada en los resultados del cálculo de los polos y ceros. Una señal de entrada con ruido o distorsión puede afectar la precisión de los resultados obtenidos.

Al calcular los polos y ceros en Matlab, es importante tener en cuenta las limitaciones del software, como la presencia de polos o ceros múltiples, la precisión numérica, los problemas con sistemas de gran tamaño, la verificación de los datos de entrada y el efecto de la calidad de la señal. Estar consciente de estos posibles errores te permitirá obtener resultados más precisos y confiables.

Existen recursos adicionales o herramientas útiles para calcular los polos y ceros en Matlab

Además de los comandos y funciones incorporados en Matlab, existen algunos recursos adicionales y herramientas útiles que pueden facilitar el cálculo de polos y ceros. Estos recursos pueden ayudarte a visualizar y analizar mejor los resultados obtenidos.

Una de las herramientas más populares es el Control System Toolbox, que proporciona una amplia gama de funciones y herramientas para el análisis y diseño de sistemas de control. Entre las funciones más útiles se encuentran zpk, tf y ss, las cuales permiten definir y manipular sistemas en diferentes representaciones.

Otra herramienta útil es la Signal Processing Toolbox, que contiene funciones para el análisis y procesamiento de señales. Algunas funciones importantes para calcular polos y ceros en esta toolbox son roots y poly, que permiten encontrar las raíces de un polinomio y construir un polinomio a partir de sus raíces, respectivamente.

Además de estas herramientas incorporadas en Matlab, también puedes encontrar recursos adicionales en la comunidad de Matlab. En la página web oficial de Matlab, existe una sección de File Exchange donde los usuarios pueden compartir y descargar scripts, funciones y herramientas desarrolladas por la comunidad. Esta comunidad es una excelente fuente de recursos y puede proporcionarte soluciones específicas para tus necesidades de cálculo de polos y ceros.

Contar con recursos adicionales y herramientas útiles puede ayudarte a calcular polos y ceros de manera más eficiente y precisa en Matlab. Tanto el Control System Toolbox como la Signal Processing Toolbox proporcionan funciones y herramientas valiosas para el análisis y diseño de sistemas de control y el procesamiento de señales. Además, la comunidad de Matlab ofrece recursos adicionales a través de su página web oficial y la sección de File Exchange.

Preguntas frecuentes (FAQ)

1. ¿Qué es un polo en Matlab?

Un polo en Matlab es un valor que hace que la función de transferencia de un sistema tenga una respuesta sinusoidal amortiguada o no amortiguada.

2. ¿Qué es un cero en Matlab?

Un cero en Matlab es un valor que hace que la función de transferencia de un sistema tenga un cero en la respuesta de frecuencia.

3. ¿Cómo puedo calcular los polos y ceros en Matlab?

En Matlab, puedes calcular los polos y ceros de una función de transferencia utilizando la función "tfdata".

4. ¿Qué información me proporcionan los polos y ceros de un sistema en Matlab?

Los polos y ceros de un sistema en Matlab te proporcionan información sobre la estabilidad y el comportamiento de frecuencia del sistema.

5. ¿Cómo puedo representar gráficamente los polos y ceros de un sistema en Matlab?

En Matlab, puedes representar gráficamente los polos y ceros de un sistema utilizando la función "pzmap".