
Calcula el mínimo relativo de una función con MATLAB: guía paso a paso
La optimización de funciones es una parte esencial de la matemática y de muchas áreas de la ciencia y la ingeniería. Encontrar el mínimo relativo de una función es uno de los problemas más comunes en esta área, y MATLAB es una herramienta poderosa para resolverlo.
Te guiaré paso a paso a través del proceso de calcular el mínimo relativo de una función usando MATLAB. Te explicaré los conceptos básicos, cómo definir una función en MATLAB, cómo utilizar la función 'fminbnd' para encontrar el mínimo relativo y cómo interpretar los resultados obtenidos. Si estás interesado en aprender cómo aprovechar al máximo las capacidades de MATLAB para resolver problemas de optimización, ¡sigue leyendo!
- Cómo se define el mínimo relativo de una función
- Cuál es la importancia de encontrar el mínimo relativo de una función
- Cuáles son las ventajas de utilizar MATLAB para calcular el mínimo relativo de una función
- Cuáles son los pasos básicos para calcular el mínimo relativo de una función con MATLAB
- Qué herramientas y funciones de MATLAB son útiles para esta tarea
- Cuál es la sintaxis básica para calcular el mínimo relativo de una función en MATLAB
- Cuáles son los posibles errores o problemas que pueden surgir al calcular el mínimo relativo de una función con MATLAB y cómo solucionarlos
- Cuáles son algunos ejemplos prácticos de cómo calcular el mínimo relativo de una función con MATLAB
- Cuáles son algunas recomendaciones adicionales para optimizar el proceso de cálculo del mínimo relativo de una función con MATLAB
- Cuáles son las aplicaciones y áreas de estudio en las que se utiliza el cálculo del mínimo relativo de una función con MATLAB
-
Preguntas frecuentes (FAQ)
- 1. ¿Qué es un mínimo relativo de una función?
- 2. ¿Cómo puedo encontrar el mínimo relativo de una función con MATLAB?
- 3. ¿Cuál es la sintaxis de la función 'fmincon' en MATLAB?
- 4. ¿Puedo usar 'fmincon' para encontrar el mínimo relativo de cualquier función?
- 5. ¿Puedo visualizar el mínimo relativo de una función con MATLAB?
Cómo se define el mínimo relativo de una función
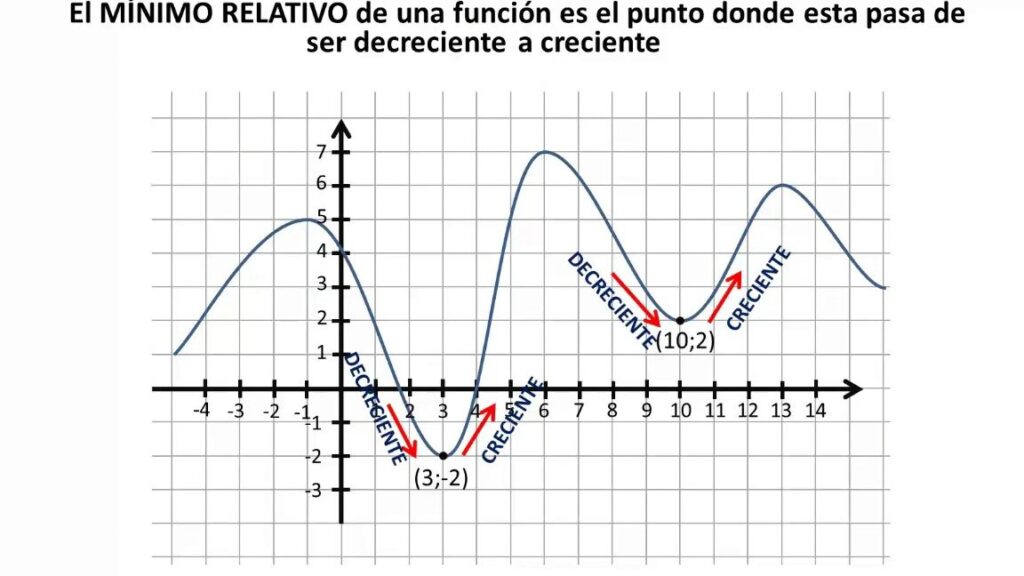
El mínimo relativo de una función se define como el valor más bajo que toma la función en un punto específico del dominio, donde la pendiente de la función es igual a cero. Esto implica que en ese punto, la función alcanza un mínimo local. Sin embargo, el valor de la función en ese punto puede no ser el mínimo absoluto. Para encontrar el mínimo relativo de una función, se debe utilizar una técnica llamada optimización, que busca el valor mínimo dentro de un rango determinado.
Pasos para calcular el mínimo relativo de una función en MATLAB
Para calcular el mínimo relativo de una función en MATLAB, se pueden seguir los siguientes pasos:
- Paso 1: Definir la función
- Paso 2: Crear un vector de puntos en el dominio
- Paso 3: Calcular la derivada de la función
- Paso 4: Encontrar los puntos críticos de la función
- Paso 5: Evaluar la segunda derivada en los puntos críticos
- Paso 6: Identificar los mínimos relativos
El primer paso para calcular el mínimo relativo de una función en MATLAB es definir la función utilizando la sintaxis adecuada. Esto implica definir la función como una función anónima o utilizar una función previamente definida.
A continuación, se debe crear un vector de puntos en el dominio de la función. Este vector de puntos será utilizado para evaluar la función y encontrar su valor mínimo relativo.
Posteriormente, se debe calcular la derivada de la función utilizando la función diff de MATLAB. Esto permitirá encontrar los puntos críticos de la función, donde la derivada es igual a cero.
Una vez encontrados los puntos críticos, se debe evaluar la segunda derivada en estos puntos. La segunda derivada permitirá determinar si los puntos críticos corresponden a mínimos relativos, máximos relativos o puntos de inflexión.
Finalmente, se debe identificar los mínimos relativos de la función utilizando los resultados obtenidos en los pasos anteriores. Estos serán los valores más bajos que toma la función en los puntos críticos encontrados.
Cuál es la importancia de encontrar el mínimo relativo de una función
En el campo de las matemáticas y la ciencia de datos, encontrar el mínimo relativo de una función es de vital importancia. Este valor representa el punto mínimo en el que la función alcanza su valor más bajo dentro de un intervalo específico.
En muchos casos, el mínimo relativo de una función tiene un significado práctico y nos permite tomar decisiones informadas en diferentes áreas, como la optimización de recursos, el diseño de experimentos o la predicción de datos.
Por lo tanto, conocer cómo calcular el mínimo relativo de una función utilizando MATLAB puede ser una herramienta invaluable para cualquier persona involucrada en el análisis de datos o la resolución de problemas matemáticos.
Cuáles son las ventajas de utilizar MATLAB para calcular el mínimo relativo de una función
Utilizar MATLAB para calcular el mínimo relativo de una función tiene varias ventajas. En primer lugar, MATLAB es un lenguaje de programación muy versátil y potente que permite realizar cálculos matemáticos de manera eficiente. Además, cuenta con una amplia gama de funciones y herramientas específicas para el análisis numérico y la optimización, lo cual facilita el proceso de encontrar el mínimo relativo de una función. Otra ventaja es que MATLAB proporciona una interfaz gráfica intuitiva que permite visualizar los resultados de manera clara y precisa. Esto es especialmente útil para comprender y analizar los resultados obtenidos. También, MATLAB es ampliamente utilizado en el ámbito académico y profesional, lo que significa que hay una gran cantidad de recursos y documentación disponibles para aprender y resolver cualquier duda durante el proceso de cálculo del mínimo relativo de una función.
Utilizar MATLAB para calcular el mínimo relativo de una función ofrece ventajas como su versatilidad, las herramientas y funciones específicas para análisis numérico y optimización, la interfaz gráfica intuitiva y la abundante documentación y recursos disponibles. Estas ventajas hacen de MATLAB una herramienta efectiva y eficiente para encontrar el mínimo relativo de una función.
Cuáles son los pasos básicos para calcular el mínimo relativo de una función con MATLAB
Para calcular el mínimo relativo de una función con MATLAB, hay algunos pasos básicos que debes seguir. En primer lugar, debes definir la función que deseas analizar utilizando la sintaxis adecuada de MATLAB. Luego, puedes utilizar la función 'fminsearch' para encontrar el mínimo relativo de la función. Esta función utiliza el algoritmo de búsqueda en una dirección conocido como 'Simplex Nelder-Mead' para encontrar el mínimo. A continuación, es importante establecer los parámetros iniciales adecuados para la función 'fminsearch'. Esto se puede hacer utilizando una evaluación inicial de la función en diferentes puntos. Finalmente, debes utilizar los resultados obtenidos para interpretar y visualizar el mínimo relativo de la función en un gráfico. Esto puede incluir trazar la función y el punto mínimo relativo.
Una vez que tengas claro estos pasos básicos, puedes comenzar a calcular el mínimo relativo de cualquier función en MATLAB. Sin embargo, ten en cuenta que hay varias consideraciones adicionales a tener en cuenta, como la elección de los puntos iniciales y los límites de búsqueda. Además, puede ser útil familiarizarse con otros métodos de optimización disponibles en MATLAB, como 'fminunc', que utiliza el algoritmo de gradiente descendente para encontrar el mínimo global de una función. En última instancia, el cálculo del mínimo relativo de una función con MATLAB requiere un enfoque analítico y práctico para obtener resultados precisos y significativos.
Paso 1: Definir la función a analizar
Antes de calcular el mínimo relativo de una función, debes primero definir la función que deseas analizar en MATLAB. Esto se puede hacer utilizando la sintaxis adecuada de MATLAB para definir una función, utilizando variables simbólicas si es necesario. Una vez que hayas definido la función, puedes proceder a los pasos siguientes para calcular el mínimo relativo.
Paso 2: Utilizar la función 'fminsearch'
La función 'fminsearch' es una herramienta útil en MATLAB para encontrar el mínimo relativo de una función. Esta función utiliza el algoritmo de Simplex Nelder-Mead, que es un método no lineal para la optimización no restringida. Para utilizar 'fminsearch', simplemente debes llamar a la función con la sintaxis adecuada, especificando la función a minimizar y los valores iniciales para los parámetros.
Paso 3: Establecer parámetros iniciales
Es importante establecer los parámetros iniciales adecuados para la función 'fminsearch'. Esto se puede hacer utilizando una evaluación inicial de la función en diferentes puntos. La elección de estos puntos iniciales puede afectar el resultado final, por lo que es importante considerar cuidadosamente los valores iniciales que utilizas. Puedes probar diferentes valores iniciales para ver cómo afecta al resultado final.
Paso 4: Interpretar y visualizar los resultados
Una vez que hayas calculado el mínimo relativo de la función utilizando 'fminsearch', es importante interpretar y visualizar los resultados obtenidos. Esto se puede hacer trazando la función y el punto mínimo relativo en un gráfico. Esto te permitirá tener una mejor comprensión de la ubicación del mínimo relativo y cómo afecta a la función en general. Además, puedes utilizar los resultados obtenidos para realizar cálculos o análisis adicionales según sea necesario.
Calcular el mínimo relativo de una función con MATLAB requiere seguir algunos pasos básicos, como definir la función, utilizar la función 'fminsearch', establecer los parámetros iniciales y finalmente interpretar y visualizar los resultados. Al seguir estos pasos, podrás calcular el mínimo relativo de cualquier función de manera efectiva utilizando MATLAB.
Qué herramientas y funciones de MATLAB son útiles para esta tarea
Para calcular el mínimo relativo de una función con MATLAB, hay varias herramientas y funciones útiles que puedes utilizar. En primer lugar, necesitarás la función fminbnd, que es la función en MATLAB que permite encontrar el mínimo de una función en un intervalo dado. Además, también puedes utilizar la función fminsearch, que es una función de búsqueda de mínimo general en MATLAB. Estas funciones son especialmente útiles cuando tienes una función continua y quieres encontrar el mínimo relativo dentro de un rango dado.
Otra herramienta útil en MATLAB para calcular el mínimo relativo de una función es la función diff, que se utiliza para calcular la derivada de una función. Puedes utilizar esta función para encontrar los puntos críticos de la función, que son los puntos donde la derivada de la función es igual a cero. Estos puntos críticos son potenciales mínimos relativos. Además, puedes utilizar la función fplot para trazar la función y visualizar los puntos críticos y el mínimo relativo.
Además de estas herramientas y funciones, también es útil tener en cuenta algunos conceptos y técnicas matemáticas para la optimización de funciones. Por ejemplo, el concepto de primera y segunda derivada puede ser útil para determinar si un punto crítico es un mínimo relativo o un punto de inflexión. También puedes utilizar técnicas de optimización global, como la técnica de búsqueda de líneas o el uso de algoritmos de optimización evolutiva, para encontrar el mínimo relativo en un rango más amplio o en funciones más complejas.
Cuál es la sintaxis básica para calcular el mínimo relativo de una función en MATLAB
En MATLAB, para calcular el mínimo relativo de una función, se utiliza la función fminbnd. La sintaxis básica es la siguiente:
= fminbnd(fun, x1, x2)
Donde:
- xmin es el valor del mínimo relativo de la función.
- fmin es el valor mínimo de la función en xmin.
- fun es el nombre o el handle de la función que queremos minimizar.
- x1 y x2 son los límites inferior y superior del intervalo de búsqueda.
Una vez que hayamos definido la función y establecido los límites del intervalo, podemos llamar a la función fminbnd para calcular el mínimo relativo.
Paso 1: Definir la función a minimizar
El primer paso para calcular el mínimo relativo de una función es definir la función que queremos minimizar. Por ejemplo, si queremos encontrar el mínimo relativo de la función cuadrática f(x) = x^2 + 2x + 1, podemos definirla de la siguiente manera en MATLAB:
fun = @(x) x^2 + 2x + 1;
Esta función se define utilizando la notación de funciones anónimas de MATLAB (@(x)) y la expresión de la función cuadrática (x^2 + 2x + 1).
Paso 2: Establecer los límites del intervalo
Una vez que hemos definido la función a minimizar, necesitamos establecer los límites del intervalo de búsqueda. El mínimo relativo de la función se encuentra dentro de este intervalo.
Por ejemplo, si queremos buscar el mínimo relativo en el intervalo , podemos establecer los límites del intervalo de la siguiente manera:
x1 = -5;
x2 = 5;
Estos límites pueden ajustarse según las necesidades de la función que se está minimizando.
Paso 3: Calcular el mínimo relativo
Una vez que hemos definido la función y establecido los límites del intervalo, podemos llamar a la función fminbnd para calcular el mínimo relativo.
Usamos la sintaxis básica que mencionamos anteriormente:
= fminbnd(fun, x1, x2);
Por ejemplo, usando la función cuadrática y los límites del intervalo mencionados anteriormente:
= fminbnd(fun, -5, 5);
La función fminbnd calculará el mínimo relativo de la función y devolverá los valores de xmin y fmin.
Es importante mencionar que la función fminbnd utiliza un algoritmo de búsqueda para encontrar el mínimo relativo dentro del intervalo especificado. Por lo tanto, los resultados pueden variar dependiendo de la función y los límites del intervalo.
Cuáles son los posibles errores o problemas que pueden surgir al calcular el mínimo relativo de una función con MATLAB y cómo solucionarlos
Al utilizar MATLAB para calcular el mínimo relativo de una función, es posible que te enfrentes a algunos errores o problemas. Aquí te presentamos algunos de los más comunes y cómo solucionarlos:
Error de sintaxis
Es posible que al ingresar la función en MATLAB cometas un error de sintaxis, lo cual impedirá que puedas calcular el mínimo relativo correctamente. Asegúrate de revisar cuidadosamente el código y verificar que esté escrito correctamente, prestando especial atención a los paréntesis, comas y operadores matemáticos.
Función no diferenciable
Si estás intentando calcular el mínimo relativo de una función que no es diferenciable, MATLAB no podrá realizar el cálculo de forma automática. En este caso, tendrás que buscar otra estrategia para encontrar el mínimo, como realizar una búsqueda exhaustiva de puntos críticos o utilizar métodos numéricos avanzados.
Convergencia lenta
Algunos métodos utilizados para calcular el mínimo relativo pueden tener problemas de convergencia lenta, especialmente cuando trabajas con funciones altamente no lineales o de alta dimensionalidad. En estos casos, puedes probar ajustar los parámetros del método o utilizar algoritmos de optimización más avanzados para acelerar la convergencia.
Puntos críticos múltiples
Si la función tiene múltiples puntos críticos, es posible que MATLAB encuentre solo uno de ellos como mínimo relativo. Para obtener todos los mínimos relativos, deberás utilizar técnicas como el análisis gráfico de la función o métodos numéricos que busquen todos los puntos críticos.
Problemas de precisión numérica
En ocasiones, los métodos numéricos utilizados para calcular el mínimo relativo pueden tener problemas de precisión numérica. Esto puede manifestarse en resultados aproximados o ligeramente incorrectos. Si la precisión es crucial, deberás ajustar los parámetros del método o utilizar algoritmos más precisos.
División entre cero
En algunas funciones, es posible que te encuentres con divisiones entre cero al calcular el mínimo relativo. Esto puede ocurrir cuando la función tiene singularidades o puntos de inflexión. En tales casos, deberás identificar estas situaciones y tomar medidas para evitar la división entre cero, ya sea modificando la función o ajustando los parámetros del método de cálculo.
Estos son solo algunos de los posibles errores o problemas que pueden surgir al calcular el mínimo relativo de una función con MATLAB. Recuerda siempre verificar y revisar tus resultados, así como considerar diferentes métodos de cálculo para asegurarte de obtener resultados precisos y confiables.
Cuáles son algunos ejemplos prácticos de cómo calcular el mínimo relativo de una función con MATLAB
Calcular el mínimo relativo de una función puede ser útil en diversos escenarios. Por ejemplo, en el análisis de datos, podemos querer encontrar el punto donde una función alcanza su valor mínimo. En la optimización de procesos, identificar el mínimo relativo es esencial para mejorar la eficiencia.
Un ejemplo práctico podría ser el siguiente: supongamos que tenemos una función que representa el costo de producción de un producto en función de la cantidad producida. Queremos encontrar el punto donde el costo es mínimo, para así determinar la cantidad óptima a producir.
Otro ejemplo podría ser en el campo de la física. Supongamos que tenemos una función que describe la trayectoria de un proyectil y queremos encontrar el punto donde la altura alcanza su mínimo. Esto podría ser útil para determinar el punto más bajo de la trayectoria y evitar posibles obstáculos.
Calcular el mínimo relativo de una función con MATLAB nos proporciona información valiosa en muchos ámbitos, desde análisis de datos hasta optimización de procesos o resolución de problemas físicos. En los siguientes pasos, veremos cómo hacerlo paso a paso.
Cuáles son algunas recomendaciones adicionales para optimizar el proceso de cálculo del mínimo relativo de una función con MATLAB
Además de seguir los pasos anteriores, hay algunas recomendaciones adicionales que pueden ayudarte a optimizar el proceso de cálculo del mínimo relativo de una función con MATLAB. Aquí te las presentamos:
1. Ajusta los parámetros de tolerancia
Para obtener resultados más precisos, puedes ajustar los parámetros de tolerancia en la función de optimización de MATLAB. Esto te permitirá controlar el nivel de presición deseado en el cálculo del mínimo relativo.
2. Utiliza funciones de derivadas
Si la función que deseas optimizar es demasiado compleja para calcular su derivada analíticamente, puedes utilizar las funciones de derivadas numéricas de MATLAB. Esto te permitirá obtener una aproximación de la derivada y realizar el cálculo del mínimo relativo.
3. Experimenta con diferentes algoritmos de optimización
MATLAB ofrece una variedad de algoritmos de optimización que puedes utilizar para calcular el mínimo relativo de una función. Experimenta con diferentes opciones y evalúa cuál de ellos te proporciona los resultados más precisos y eficientes.
4. Utiliza paralelización si es posible
Si tu computadora dispone de múltiples núcleos de procesamiento, puedes utilizar la paralelización en MATLAB para acelerar el cálculo del mínimo relativo. Esto te permitirá distribuir la carga computacional en varios núcleos y reducir el tiempo de ejecución.
5. Optimiza el código
Revisa tu código y busca posibles mejoras de rendimiento. Elimina bucles innecesarios, utiliza vectorización cuando sea posible y evita el uso de variables adicionales que consuman memoria. Un código optimizado puede hacer una gran diferencia en el tiempo de cálculo del mínimo relativo.
6. Considera el uso de herramientas externas
Si la optimización de la función con MATLAB no te proporciona los resultados deseados, considera el uso de herramientas externas especializadas en optimización. Existen diversos software y bibliotecas que pueden ser de utilidad en la búsqueda del mínimo relativo de una función.
Siguiendo estas recomendaciones adicionales, podrás optimizar el proceso de cálculo del mínimo relativo de una función con MATLAB y obtener resultados más precisos y eficientes.
Cuáles son las aplicaciones y áreas de estudio en las que se utiliza el cálculo del mínimo relativo de una función con MATLAB
El cálculo del mínimo relativo de una función utilizando MATLAB tiene numerosas aplicaciones en diferentes áreas de estudio. En el campo de la ingeniería, se utiliza para optimizar diseños de estructuras, sistemas de control y análisis de señales. En física, se aplica para analizar la trayectoria de partículas en campos electromagnéticos. En economía, se utiliza para maximizar la eficiencia de la producción y minimizar costos. Además, el cálculo del mínimo relativo también se utiliza en biología para modelar interacciones entre especies y en química para determinar reacciones más eficientes.
El cálculo del mínimo relativo de una función con MATLAB tiene amplias aplicaciones en diversas áreas de estudio y es una herramienta invaluable para optimizar diseños, analizar trayectorias y maximizar la eficiencia en diferentes disciplinas.
Preguntas frecuentes (FAQ)
1. ¿Qué es un mínimo relativo de una función?
Un mínimo relativo de una función es un punto en el que la función alcanza su valor más bajo en un cierto intervalo, pero no necesariamente es el valor mínimo absoluto de la función.
2. ¿Cómo puedo encontrar el mínimo relativo de una función con MATLAB?
Puedes encontrar el mínimo relativo de una función en MATLAB utilizando la función 'fmincon'. Esta función minimiza una función sujeta a restricciones. Para encontrar el mínimo relativo, debes proporcionar la función objetivo y las restricciones adecuadas.
3. ¿Cuál es la sintaxis de la función 'fmincon' en MATLAB?
La sintaxis básica de la función 'fmincon' en MATLAB es la siguiente: = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options). Donde 'fun' es la función objetivo, 'x0' es el vector inicial de variables, 'A' y 'b' son matrices que definen restricciones lineales, 'Aeq' y 'beq' son matrices que definen restricciones lineales de igualdad, 'lb' y 'ub' son los límites inferiores y superiores de las variables, 'nonlcon' es una función que define restricciones no lineales y 'options' es una estructura que especifica opciones adicionales.
4. ¿Puedo usar 'fmincon' para encontrar el mínimo relativo de cualquier función?
'fmincon' es una función versátil y puede utilizarse para encontrar el mínimo relativo de una amplia variedad de funciones. Sin embargo, es importante tener en cuenta que 'fmincon' requiere que la función objetivo y las restricciones sean diferenciables. Por lo tanto, si tu función no es diferenciable, es posible que necesites utilizar métodos alternativos para encontrar el mínimo relativo.
5. ¿Puedo visualizar el mínimo relativo de una función con MATLAB?
Sí, puedes visualizar el mínimo relativo de una función utilizando la función 'fmincon' junto con la función 'plot'. Puedes trazar la función objetivo y marcar el mínimo relativo encontrado por 'fmincon' en el gráfico para visualizar mejor el resultado.
Deja una respuesta








Artículos que podrían interesarte