Calcula el ángulo de un vector en Matlab con solo dos puntos
Matlab es un lenguaje de programación muy utilizado en ciencias e ingeniería para realizar cálculos numéricos y análisis de datos. Una de las operaciones más comunes que se realizan en Matlab es el cálculo de ángulos, ya sea entre dos vectores o entre un vector y un eje de referencia. Aprenderemos cómo calcular el ángulo de un vector en Matlab utilizando solo dos puntos.
Te explicaré paso a paso cómo calcular el ángulo de un vector en Matlab utilizando solo dos puntos como entrada. Primero, veremos cómo definir los puntos en Matlab y cómo obtener las coordenadas x y y de cada punto. Luego, explicaré cómo calcular el ángulo utilizando la función atan2 de Matlab. Finalmente, te daré un ejemplo práctico de cómo aplicar esta técnica para calcular el ángulo entre dos puntos en un plano xy. ¡Sigue leyendo para descubrir cómo hacerlo!
¿Qué verás en este artículo?
- Cómo puedo definir un vector en Matlab utilizando solo dos puntos
- Cuál es la fórmula para calcular el ángulo entre dos vectores en Matlab
- Qué funciones puedo usar en Matlab para calcular el ángulo entre dos vectores
- Es posible calcular el ángulo de un vector en Matlab si solo tengo las coordenadas de dos puntos
- Cuál es la diferencia entre calcular el ángulo de un vector en 2D y en 3D en Matlab
- Existen métodos alternativos para calcular el ángulo de un vector en Matlab sin utilizar la fórmula tradicional
- Cómo puedo visualizar el ángulo de un vector en Matlab en forma gráfica
- Se puede calcular el ángulo de un vector en Matlab si solo tengo las coordenadas del punto inicial y la dirección del vector
- Es posible calcular el ángulo de un vector en Matlab si solo tengo las coordenadas del punto final y la dirección del vector
- Cuál es la importancia de calcular el ángulo de un vector en Matlab en aplicaciones de ingeniería y ciencias de la computación
- Preguntas frecuentes (FAQ)
Cómo puedo definir un vector en Matlab utilizando solo dos puntos
En Matlab, podemos definir un vector utilizando solo dos puntos. Para hacerlo, primero necesitamos conocer las coordenadas de estos dos puntos. Supongamos que tenemos el punto A con coordenadas (x1, y1) y el punto B con coordenadas (x2, y2).
Para calcular el vector AB en Matlab, utilizamos la fórmula:
v = ;
Donde v es el vector AB.
Esta fórmula nos permite obtener las componentes del vector AB en el sistema de coordenadas x-y. Una vez que tenemos las componentes del vector, podemos utilizarlas para realizar diferentes operaciones y cálculos en Matlab.
Cuál es la fórmula para calcular el ángulo entre dos vectores en Matlab
Para calcular el ángulo entre dos vectores en Matlab, necesitarás utilizar la fórmula del producto escalar. Esta fórmula nos permite encontrar el ángulo entre dos vectores a partir de sus componentes.
Primero, debes encontrar el producto escalar entre los dos vectores utilizando la función dot(). Por ejemplo, si tienes dos vectores A y B, puedes encontrar su producto escalar utilizando la siguiente sintaxis:
producto_escalar = dot(A, B);
A continuación, puedes encontrar las magnitudes de ambos vectores utilizando la función norm(). Por ejemplo, para encontrar la magnitud del vector A, puedes usar lo siguiente:
magnitud_A = norm(A);
De manera similar, puedes encontrar la magnitud del vector B utilizando:
magnitud_B = norm(B);
Finalmente, puedes usar la fórmula del ángulo entre dos vectores, que es:
angulo = acosd(producto_escalar / (magnitud_A magnitud_B));
La función acosd() se utiliza para calcular el arco coseno en grados. Así que el resultado de esta fórmula te dará el ángulo entre los dos vectores en grados. Recuerda que debes convertir el resultado a grados si deseas obtener una respuesta en radianes.
Qué funciones puedo usar en Matlab para calcular el ángulo entre dos vectores
En Matlab, puedes utilizar la función dot para calcular el producto punto entre dos vectores. Esto te dará el valor del coseno del ángulo entre ellos. Para obtener el ángulo en sí, puedes utilizar la función acos y convertir el resultado de radianes a grados utilizando la función rad2deg. Además, si solo tienes dos puntos y deseas encontrar el ángulo entre el vector que se forma con ellos y el eje horizontal, puedes utilizar la función atan2. Esta función te dará el ángulo en radianes y luego puedes convertirlo a grados si es necesario.
Por ejemplo, supongamos que tienes dos puntos p1 y p2 en el espacio tridimensional. Si deseas calcular el ángulo entre el vector que se forma con estos dos puntos y el eje horizontal, puedes hacerlo de la siguiente manera:
vector = p2 - p1;
angle = atan2(vector(2), vector(1));
angle_degrees = rad2deg(angle);
En este ejemplo, la variable vector contiene la diferencia entre los dos puntos en forma de un vector en el espacio tridimensional. Luego, utilizamos la función atan2 para calcular el ángulo en radianes y finalmente lo convertimos a grados utilizando la función rad2deg.
Estas funciones son muy útiles cuando necesitas calcular el ángulo entre dos vectores en Matlab. Recuerda que puedes adaptar el código según tus necesidades específicas y que siempre es recomendable leer la documentación oficial de Matlab para obtener más información sobre estas y otras funciones relacionadas.
Es posible calcular el ángulo de un vector en Matlab si solo tengo las coordenadas de dos puntos
En ocasiones, cuando trabajamos con datos en Matlab, necesitamos calcular el ángulo entre dos puntos en un espacio bidimensional. Afortunadamente, existe una forma sencilla de hacerlo utilizando las coordenadas de esos dos puntos.
Para calcular el ángulo entre dos puntos en Matlab, primero debemos encontrar el vector que une los dos puntos. Este vector se puede obtener restando las coordenadas del segundo punto a las coordenadas del primer punto.
A continuación, utilizaremos la función atan2 para calcular el ángulo entre el vector y el eje x. Esta función toma como argumentos la coordenada y y la coordenada x del vector y devuelve el ángulo correspondiente en radianes.
Finalmente, si deseamos obtener el ángulo en grados, podemos utilizar la función rad2deg para convertir el ángulo de radianes a grados.
El proceso para calcular el ángulo de un vector en Matlab con solo dos puntos es el siguiente:
- Restar las coordenadas del segundo punto a las coordenadas del primer punto para obtener el vector que une los dos puntos.
- Utilizar la función
atan2para calcular el ángulo entre el vector y el eje x. - Opcionalmente, utilizar la función
rad2degpara convertir el ángulo de radianes a grados.
Con este procedimiento, podemos calcular fácilmente el ángulo de un vector en Matlab con solo dos puntos, lo cual resulta muy útil en diversas aplicaciones.
Cuál es la diferencia entre calcular el ángulo de un vector en 2D y en 3D en Matlab
Al calcular el ángulo de un vector en 2D en Matlab, solo se consideran dos puntos que representan el vector. Estos puntos están ubicados en un plano bidimensional, lo que significa que solo se tiene en cuenta el desplazamiento horizontal y vertical.
Por otro lado, al calcular el ángulo de un vector en 3D en Matlab, se necesitan tres puntos que representan el vector. Estos puntos están ubicados en un espacio tridimensional, lo que implica tener en cuenta el desplazamiento en tres dimensiones: horizontal, vertical y profundidad.
La principal diferencia entre calcular el ángulo de un vector en 2D y en 3D en Matlab radica en la cantidad de puntos necesarios para representar el vector y en las dimensiones del espacio en el que se encuentra el vector.
Existen métodos alternativos para calcular el ángulo de un vector en Matlab sin utilizar la fórmula tradicional
Si bien es común calcular el ángulo de un vector utilizando la fórmula tradicional, existen otros métodos que pueden simplificar este proceso en Matlab. Uno de estos métodos es utilizando la función acosd, que permite obtener directamente el ángulo en grados entre dos vectores. Otra opción es utilizar la función atan2, que devuelve el ángulo en radianes y tiene en cuenta el cuadrante en el que se encuentra el vector resultante. De esta manera, podemos calcular el ángulo con mayor precisión y evitar errores comunes.
Para utilizar la función acosd, debemos asegurarnos de que los vectores estén normalizados. Si no lo están, podemos utilizar la función norm para normalizarlos. A continuación, podemos utilizar la función dot para obtener el producto escalar de los dos vectores normalizados. Finalmente, aplicamos la función acosd al producto escalar para obtener el ángulo en grados.
Ejemplo de cálculo del ángulo utilizando la función acosd:
v1 = ;
v2 = ;
v1_norm = v1 / norm(v1);
v2_norm = v2 / norm(v2);
angle = acosd(dot(v1_norm, v2_norm));
Para utilizar la función atan2, simplemente debemos pasar como argumento los componentes del vector en el eje x y el eje y. Esta función retorna el ángulo en radianes, teniendo en cuenta el cuadrante en el que se encuentra el vector resultante. Podemos utilizar la función radtodeg para convertir el resultado a grados si lo deseamos.
Ejemplo de cálculo del ángulo utilizando la función atan2:
v1 = ;
v2 = ;
angle_rad = atan2(v2(2), v2(1)) - atan2(v1(2), v1(1));
angle_deg = radtodeg(angle_rad);
Estos métodos alternativos nos permiten calcular el ángulo de un vector en Matlab de manera más sencilla y precisa. Ya no es necesario utilizar la fórmula tradicional y nos evita cometer errores comunes en el cálculo. Aprovecha estas funciones y simplifica tus cálculos en Matlab.
Cómo puedo visualizar el ángulo de un vector en Matlab en forma gráfica
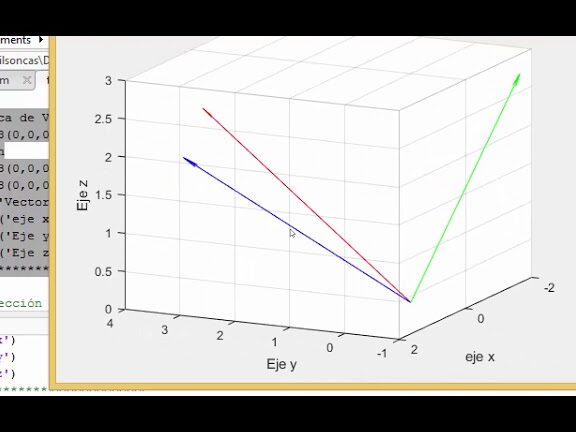
En Matlab, calcular y visualizar el ángulo de un vector de forma gráfica es posible utilizando la función "quiver". Esta función traza flechas en un gráfico 2D o 3D para representar vectores. Para calcular el ángulo de un vector, necesitamos tener las coordenadas de dos puntos que definen el vector.
Primero, definimos los puntos en el espacio utilizando las coordenadas x y y. Luego, utilizamos la función "quiver" para trazar el vector correspondiente a esos puntos.
x = ;
y = ;
quiver(x(1), y(1), x(2)-x(1), y(2)-y(1));
Este código traza una flecha que muestra el vector en el gráfico.
Ahora, para calcular el ángulo entre dos vectores, podemos utilizar la función "atan2" de Matlab, que devuelve el ángulo en radianes entre -pi y pi.
angle = atan2(y(2)-y(1), x(2)-x(1));
Podemos convertir el ángulo a grados multiplicando por 180/pi:
angle_deg = angle 180/pi;
Ahora que hemos calculado el ángulo, podemos agregarlo a la flecha trazada utilizando la función "text" de Matlab:
text(x(1)+0.5, y(1)+0.5, num2str(angle_deg));
Esto agrega el ángulo en grados al gráfico, cerca de la flecha trazada.
Para visualizar el ángulo de un vector en Matlab, primero necesitamos definir los puntos que definen el vector. Luego, utilizamos las funciones "quiver" y "text" para trazar el vector y agregar el ángulo al gráfico.
Se puede calcular el ángulo de un vector en Matlab si solo tengo las coordenadas del punto inicial y la dirección del vector
En ocasiones, podemos encontrarnos con situaciones en las que solo tenemos disponible el punto inicial y la dirección de un vector en lugar de sus coordenadas completas. Aunque esta información puede parecer limitada, gracias a Matlab podemos calcular el ángulo de dicho vector de manera sencilla.
Para ello, utilizaremos la función atan2 de Matlab, que nos permite obtener el ángulo en radianes a partir de las coordenadas x e y de un vector. Esta función es especialmente útil cuando solo tenemos la dirección de un vector y deseamos calcular su ángulo.
El siguiente código muestra cómo podemos calcular el ángulo de un vector en Matlab utilizando solo el punto inicial y la dirección del vector:
% Definimos el punto inicial del vector
x0 = 0;
y0 = 0;
% Definimos la dirección del vector
dx = 2;
dy = 3;
% Calculamos el ángulo del vector
angulo = atan2(dy, dx);
% Convertimos el ángulo a grados
angulo_grados = rad2deg(angulo);
% Mostramos el resultado
fprintf('El ángulo del vector es: %.2f gradosn', angulo_grados);
En este ejemplo, hemos definido el punto inicial del vector como (0, 0) y la dirección del vector como (2, 3). Utilizando la función atan2, calculamos el ángulo del vector en radianes, y luego lo convertimos a grados utilizando la función rad2deg. Por último, mostramos el resultado por pantalla.
Es importante destacar que la función atan2 nos devuelve un ángulo en el rango de -π a π, por lo que no es necesario realizar ninguna conversión adicional. Sin embargo, si deseamos obtener el ángulo en grados, debemos utilizar la función rad2deg para convertirlo.
Si solo tienes disponible el punto inicial y la dirección de un vector, puedes calcular su ángulo utilizando la función atan2 de Matlab. Esto te permite obtener información importante sobre la orientación de tus vectores y utilizarla en tus cálculos y análisis de datos.
Es posible calcular el ángulo de un vector en Matlab si solo tengo las coordenadas del punto final y la dirección del vector
En Matlab, es posible calcular el ángulo de un vector si solo tienes las coordenadas del punto final y la dirección del vector. Para ello, es necesario utilizar algunas funciones y fórmulas matemáticas.
Primero, debes calcular las coordenadas x e y del vector utilizando la fórmula:
x = punto_final_x - punto_inicial_x;
y = punto_final_y - punto_inicial_y;
A continuación, puedes utilizar la función atan2 para calcular el ángulo en radianes:
angulo_radianes = atan2(y, x);
Si deseas obtener el ángulo en grados, puedes utilizar la función rad2deg:
angulo_grados = rad2deg(angulo_radianes);
Una vez que hayas calculado el ángulo, puedes utilizarlo en tus cálculos o mostrarlo en la pantalla:
disp();
Recuerda que en Matlab, los ángulos suelen medirse en radianes, por lo que es importante convertirlos si necesitas utilizar grados.
Puedes calcular el ángulo de un vector en Matlab utilizando las coordenadas del punto final y la dirección del vector. Utiliza las fórmulas y funciones mencionadas para obtener el resultado en radianes o grados, según tus necesidades.
Cuál es la importancia de calcular el ángulo de un vector en Matlab en aplicaciones de ingeniería y ciencias de la computación
El cálculo del ángulo de un vector en Matlab es una tarea fundamental en muchas aplicaciones de ingeniería y ciencias de la computación. Conocer el ángulo de un vector es esencial para determinar su dirección y orientación en relación con otros vectores o referencias espaciales.
En ingeniería, el cálculo del ángulo de un vector es especialmente importante en áreas como la robótica, la visión por computadora y el procesamiento de señales. En la robótica, por ejemplo, es necesario determinar el ángulo de los vectores para planificar rutas de movimiento y controlar la orientación de los manipuladores robóticos.
En ciencias de la computación, el cálculo del ángulo de un vector es crucial en algoritmos de reconocimiento de imágenes y detección de objetos. Por ejemplo, en la detección de rostros, se utiliza el ángulo entre vectores para determinar la orientación del rostro y realizar un seguimiento preciso.
El cálculo del ángulo de un vector en Matlab es esencial para una amplia gama de aplicaciones en ingeniería y ciencias de la computación. Proporciona información crítica sobre la dirección y orientación de los vectores, lo que permite tomar decisiones informadas y realizar tareas específicas en diferentes dominios.
Preguntas frecuentes (FAQ)
¿Qué es un ángulo de un vector?
El ángulo de un vector es la medida de la dirección en la que apunta el vector en relación con un punto de referencia. Se expresa en grados o radianes.
¿Cómo puedo calcular el ángulo de un vector en Matlab?
Puedes utilizar la función atan2 en Matlab para calcular el ángulo de un vector dado dos puntos. Esta función devuelve el ángulo en radianes.
¿Cuál es la sintaxis de la función atan2 en Matlab?
La sintaxis de la función atan2 en Matlab es la siguiente: ang = atan2(y, x), donde x y y son las coordenadas del punto final del vector.
¿Cómo puedo convertir el ángulo de radianes a grados en Matlab?
Para convertir el ángulo de radianes a grados en Matlab, puedes utilizar la función rad2deg. Por ejemplo, ang_grados = rad2deg(ang_rad).
¿Dónde puedo encontrar más información sobre el cálculo de ángulos en Matlab?
Puedes consultar la documentación oficial de Matlab para obtener más información sobre el cálculo de ángulos y el uso de la función atan2.
Calcula la derivada por definición en MATLAB: paso a paso
Añade columna al inicio de un vector en MATLAB: guía fácil y rápida
Conviértete en un experto: Cómo crear un array de 0 a 1 en MATLAB
Encuentra fácilmente el valor mínimo en un array cell en MATLAB
Abre tus ficheros de forma rápida y sencilla con este script de Matlab
Elimina archivos de una carpeta con Matlab de forma sencilla
Elevar 10 a un número en MATLAB: La guía definitiva sin complicaciones
Aprende fácilmente a calcular las soluciones de una función con MATLAB
Calcula la media de un vector en Matlab fácilmente paso a paso
Deja una respuesta
Artículos que podrían interesarte