Calcula armónicos en función del tiempo con MATLAB: guía informativa

Cuáles son las principales aplicaciones de la técnica de cálculo de armónicos en MATLAB

La técnica de cálculo de armónicos en MATLAB tiene una amplia gama de aplicaciones en diferentes campos. Una de las principales áreas en las que se utiliza es en la ingeniería eléctrica, específicamente en el análisis de sistemas de potencia. Con esta técnica, es posible determinar las diferentes frecuencias que componen una señal eléctrica, lo que resulta fundamental para el diseño y la optimización de sistemas de generación y distribución de energía.

Otra aplicación importante de esta técnica es en el campo de la acústica y la música. En la producción y grabación de música, el cálculo de armónicos es utilizado para analizar y sintetizar diferentes instrumentos musicales y voces. Además, permite entender la estructura armónica de una pieza musical y realizar ajustes para mejorar la calidad del sonido.

En el ámbito de las comunicaciones, la técnica de cálculo de armónicos en MATLAB es fundamental para el análisis de señales y la detección de patrones. Por ejemplo, en la transmisión de datos, es posible identificar y corregir errores utilizando esta técnica, garantizando una comunicación más efectiva y precisa.

Por último, pero no menos importante, el cálculo de armónicos en MATLAB también se utiliza en el campo de la medicina, específicamente en el análisis de señales biológicas. Esta técnica permite analizar el ritmo cardíaco, la actividad cerebral y otras señales biológicas, proporcionando información valiosa para el diagnóstico y tratamiento de enfermedades.

Cuál es el proceso paso a paso para calcular armónicos en función del tiempo con MATLAB

Calcula armónicos en función del tiempo puede parecer algo complejo, pero con MATLAB es mucho más sencillo de lo que imaginas. Aquí te presentamos un proceso paso a paso para que puedas realizar este cálculo de manera efectiva.

Paso 1: Preparación de los datos

Lo primero que necesitas hacer es preparar tus datos. Esto implica tener una serie de puntos de datos que representen la amplitud de la señal en diferentes momentos en el tiempo. Estos datos deben estar organizados en un vector o matriz en MATLAB.

Paso 2: Calcular la transformada de Fourier

Una vez que tienes tus datos preparados, puedes utilizar la función fft de MATLAB para calcular la transformada de Fourier de la señal. Esto te dará la representación en el dominio de la frecuencia de la señal, mostrando las diferentes componentes armónicas presentes.

Paso 3: Identificar los armónicos principales

Una vez que tienes la transformada de Fourier de la señal, puedes identificar los armónicos principales. Estos son los picos más altos en el espectro de frecuencia. Puedes utilizar la función findpeaks de MATLAB para identificar estos picos y obtener sus valores y frecuencias correspondientes.

Paso 4: Calcular los armónicos en función del tiempo

Una vez que tienes los valores y frecuencias de los armónicos principales, puedes utilizar la siguiente fórmula para calcular la amplitud de cada armónico en función del tiempo:

A(t) = A0 cos(2 pi f t + phi)

Donde A(t) es la amplitud en función del tiempo, A0 es la amplitud del armónico, f es la frecuencia del armónico y t es el tiempo.

Paso 5: Visualizar los resultados

Por último, puedes utilizar la función plot de MATLAB para visualizar los resultados. Puedes graficar la amplitud de cada armónico en función del tiempo para tener una representación visual de cómo varían en el tiempo.

Recuerda que este es solo un proceso básico para calcular armónicos en función del tiempo con MATLAB. Dependiendo de tus necesidades y del tipo de señal que estés analizando, es posible que necesites realizar ajustes adicionales.

Cuáles son las principales funciones y herramientas disponibles en MATLAB para el cálculo de armónicos

En MATLAB, existen varias funciones y herramientas que se pueden utilizar para el cálculo de armónicos en función del tiempo. Una de las principales funciones es la función fft, que calcula la Transformada Rápida de Fourier de una señal. Esta función es especialmente útil para analizar el espectro de frecuencia de una señal y encontrar los componentes armónicos.

Otra función importante en MATLAB es la función ifft, que realiza la Inversa de la Transformada Rápida de Fourier. Esta función se utiliza para reconstruir una señal a partir de sus componentes armónicos y es útil para sintetizar señales.

Además de estas funciones, MATLAB también cuenta con herramientas de visualización poderosas, como la función plot, que permite graficar señales en el dominio del tiempo o de la frecuencia. También se pueden utilizar otras funciones como spectrogram para visualizar el espectrograma de una señal y encontrar patrones armónicos.

MATLAB ofrece varias funciones y herramientas para el cálculo de armónicos en función del tiempo. Estas funciones y herramientas permiten realizar análisis de frecuencia, sintetizar señales y visualizar patrones armónicos, lo que facilita el estudio y la comprensión de las señales en el dominio del tiempo.

Cuáles son las ventajas de utilizar MATLAB para calcular armónicos en función del tiempo en comparación con otras herramientas

Una de las principales ventajas de utilizar MATLAB para calcular armónicos en función del tiempo es su amplia gama de funciones y herramientas especializadas en análisis de señales. MATLAB proporciona funciones específicas para calcular la transformada de Fourier y la serie de Fourier, lo que facilita el cálculo de armónicos en función del tiempo.

Otra ventaja clave es la facilidad de uso. MATLAB posee una sintaxis clara y legible, lo que permite a los usuarios escribir y comprender fácilmente el código necesario para realizar los cálculos de armónicos en función del tiempo.

Además, MATLAB ofrece una amplia gama de visualizaciones y gráficos personalizables, lo que facilita la interpretación y análisis de los resultados obtenidos.

Por último, MATLAB cuenta con una gran comunidad de usuarios y una amplia documentación, lo que permite obtener apoyo y solucionar cualquier problema o duda que pueda surgir durante el proceso de cálculo de armónicos en función del tiempo.

Qué tipos de señales eléctricas y electrónicas son más propensas a tener armónicos y cómo identificarlos en MATLAB

Las señales eléctricas y electrónicas que son más propensas a tener armónicos son aquellas que contienen componentes de frecuencia múltiples de la frecuencia fundamental. Estos armónicos pueden generar distorsiones en la señal y afectar su calidad. Afortunadamente, MATLAB ofrece herramientas y funciones que nos permiten identificar y analizar los armónicos presentes en una señal.

Para identificar los armónicos en MATLAB, primero debemos cargar la señal de interés en el entorno de trabajo utilizando la función "load". A continuación, podemos utilizar la transformada de Fourier para obtener la representación espectral de la señal. La función "fft" nos permite realizar esta transformada de manera rápida y eficiente.

Una vez obtenida la representación espectral de la señal, podemos visualizarla utilizando la función "plot". Esto nos mostrará las amplitudes de los diferentes componentes de frecuencia presentes en la señal. Si observamos picos en las frecuencias múltiples de la frecuencia fundamental, podemos concluir que hay armónicos presentes en la señal.

Además de identificar los armónicos, también podemos calcular su magnitud utilizando la función "abs" y su fase utilizando la función "angle". Esto nos brinda información adicional sobre la naturaleza de los armónicos presentes en la señal.

MATLAB nos proporciona las herramientas necesarias para identificar y analizar los armónicos en señales eléctricas y electrónicas. Al comprender la presencia y la magnitud de los armónicos, podemos tomar medidas adecuadas para mitigar sus efectos y mejorar la calidad de las señales.

Cómo interpretar los resultados obtenidos al calcular armónicos en función del tiempo con MATLAB

Una vez que hayas realizado el cálculo de los armónicos en función del tiempo utilizando MATLAB, es importante poder interpretar correctamente los resultados obtenidos. Esto te permitirá comprender el comportamiento de las señales y extraer información relevante de ellas.

En primer lugar, es fundamental entender que los armónicos representan las componentes frecuenciales de una señal. Cada armónico se caracteriza por una frecuencia específica y una amplitud determinada. Al realizar el cálculo, obtendrás los armónicos presentes en la señal y su correspondiente amplitud en función del tiempo.

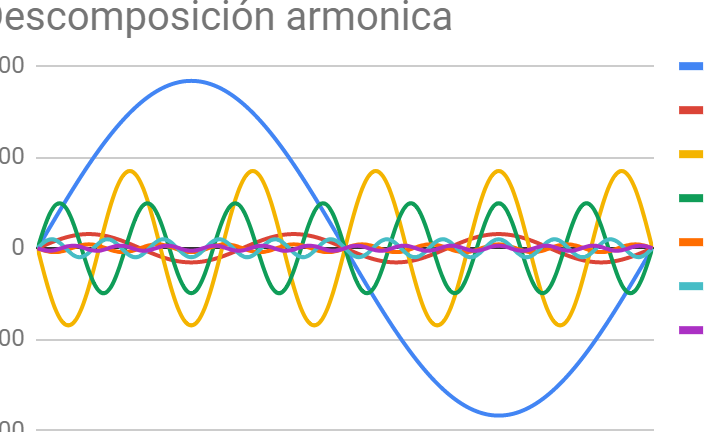
Una forma común de representar los resultados es mediante un gráfico en el que en el eje vertical se muestre la amplitud y en el eje horizontal el tiempo. Cada armónico será representado por una curva en el gráfico, y su altura indicará la amplitud correspondiente en función del tiempo.

Es importante tener en cuenta que la interpretación de los resultados puede variar dependiendo del tipo de señal que estés analizando. Por ejemplo, si estás trabajando con una señal de audio, los armónicos pueden representar notas musicales o frecuencias específicas presentes en dicha señal.

En el caso de señales más complejas, como por ejemplo las señales de radio, los armónicos pueden corresponder a diferentes canales o frecuencias utilizadas para la transmisión de información.

Además de la amplitud y frecuencia de los armónicos, otro parámetro importante a tener en cuenta es la fase. La fase determina el desfase temporal de cada armónico con respecto a una señal de referencia. Esto puede ser relevante en aplicaciones donde se requiera sincronización o alineación temporal de diferentes señales.

Al interpretar los resultados obtenidos al calcular armónicos en función del tiempo con MATLAB, es esencial considerar la amplitud, frecuencia y fase de cada armónico. Esto te permitirá comprender el comportamiento de la señal analizada y extraer información relevante para tu aplicación específica.

Qué estrategias se pueden utilizar para mitigar los efectos negativos de los armónicos en sistemas eléctricos y electrónicos

Los armónicos pueden causar problemas en sistemas eléctricos y electrónicos, como distorsión de la forma de onda, calentamiento excesivo de componentes y pérdida de eficiencia. Para mitigar estos efectos, se pueden emplear diversas estrategias.

1. Filtros de armónicos:

Una opción es utilizar filtros para limitar las frecuencias de armónicos no deseados. Estos filtros se colocan en paralelo con la carga afectada y pueden ser pasivos o activos.

2. Transformadores de potencia:

Los transformadores de potencia con devanados múltiples pueden ayudar a reducir los armónicos. Estos transformadores se diseñan de manera especial para atenuar las corrientes de armónicos.

3. Uso de convertidores activos:

Los convertidores activos pueden corregir los armónicos generados por cargas no lineales. Estos dispositivos inyectan corrientes de magnitud y fase opuestas a las corrientes de armónicos, cancelándolas.

4. Mejora del diseño del sistema:

Otra estrategia es realizar un diseño adecuado del sistema eléctrico o electrónico. Esto implica minimizar la longitud de los cables, utilizar conductores de mayor sección y evitar la colocación de cargas no lineales cerca de componentes sensibles.

5. Educación y concienciación:

Es importante educar a los usuarios y operadores de sistemas eléctricos y electrónicos sobre los efectos de los armónicos y las medidas para mitigarlos. El conocimiento y la concienciación pueden ayudar a prevenir problemas y optimizar el rendimiento de los sistemas.

6. Cumplir con las normativas:

Es fundamental cumplir con las normativas y estándares relacionados con los armónicos. Estas regulaciones establecen límites máximos admisibles de armónicos en diferentes tipos de sistemas.

Conclusiones:

Los armónicos representan una preocupación en sistemas eléctricos y electrónicos, pero con las estrategias adecuadas se pueden mitigar sus efectos negativos. La combinación de filtros, transformadores, convertidores activos, un diseño óptimo, educación y cumplimiento de normativas puede ayudar a garantizar un funcionamiento eficiente y confiable de los sistemas.

Cuáles son los desafíos comunes al calcular armónicos en función del tiempo y cómo superarlos utilizando MATLAB

Al calcular armónicos en función del tiempo, es común enfrentar varios desafíos. Uno de ellos es la complejidad matemática de los cálculos involucrados, especialmente cuando se trata de señales complejas. Otro desafío es la gestión adecuada de los datos, ya que se requiere procesar y analizar grandes cantidades de información.

Una forma de superar estos desafíos es utilizando MATLAB, una poderosa herramienta de computación numérica. MATLAB ofrece una amplia gama de funciones y herramientas diseñadas específicamente para el cálculo de armónicos en función del tiempo.

Utilizando las funciones incorporadas de MATLAB

Una de las ventajas de MATLAB es la amplia variedad de funciones incorporadas que facilitan el cálculo de armónicos en función del tiempo. Por ejemplo, la función fft se utiliza comúnmente para calcular la transformada rápida de Fourier, que es fundamental para analizar señales y extraer información armónica. También existen funciones para calcular el espectro de potencia, identificar picos armónicos y realizar otros cálculos necesarios para el análisis de armónicos en función del tiempo.

Además de las funciones incorporadas, MATLAB también ofrece herramientas para visualizar y analizar los resultados de los cálculos de armónicos. La función plot permite trazar gráficos, lo que facilita la comprensión de los resultados. MATLAB también cuenta con herramientas para realizar análisis estadísticos y generar informes detallados.

Aplicaciones prácticas del cálculo de armónicos en función del tiempo

El cálculo de armónicos en función del tiempo tiene numerosas aplicaciones prácticas en diversos campos. En la industria de la música, por ejemplo, es crucial para el diseño y la fabricación de instrumentos musicales. También es utilizado en el procesamiento de señales de audio y video, así como en el análisis de señales biomédicas.

Otra aplicación importante es en la ingeniería eléctrica, donde el cálculo de armónicos en función del tiempo es esencial para el diseño y la optimización de sistemas de generación y distribución de energía. También se utiliza en el análisis de la calidad de la energía eléctrica y en la detección de problemas en el suministro de energía.

El cálculo de armónicos en función del tiempo es un área de estudio importante con numerosas aplicaciones prácticas. MATLAB ofrece una amplia gama de funciones y herramientas para facilitar estos cálculos, lo que permite superar los desafíos comunes asociados con la complejidad matemática y la gestión de datos. Al utilizar MATLAB, los ingenieros y científicos pueden realizar análisis de armónicos de manera eficiente y obtener resultados precisos para una variedad de aplicaciones.

Existen ejemplos prácticos o casos de estudio disponibles para aprender más sobre el cálculo de armónicos en función del tiempo con MATLAB

Si estás interesado en aprender más sobre el cálculo de armónicos en función del tiempo con MATLAB, existen varios ejemplos prácticos y casos de estudio disponibles que pueden ayudarte a comprender mejor este concepto.

Uno de los ejemplos más comunes es el cálculo de armónicos en señales de corriente o voltaje en sistemas eléctricos. MATLAB ofrece herramientas y funciones específicas para analizar y calcular estos armónicos, lo que resulta útil para el diseño y mantenimiento de sistemas de energía eléctrica.

Otro ejemplo práctico es el cálculo de armónicos en señales de audio. Si estás interesado en el procesamiento de señales de audio y música, MATLAB ofrece una amplia gama de herramientas y funciones que te permitirán analizar y calcular los armónicos presentes en una señal de audio.

Además, existen casos de estudio disponibles en la documentación oficial de MATLAB, así como en diferentes recursos en línea, donde se explican paso a paso los procedimientos para calcular armónicos en función del tiempo en diferentes aplicaciones y situaciones.

Si deseas aprender más sobre el cálculo de armónicos en función del tiempo con MATLAB, te recomendaría explorar los ejemplos prácticos y casos de estudio disponibles en la documentación oficial y otros recursos en línea, ya que te brindarán una comprensión más profunda de este tema.

Preguntas frecuentes (FAQ)

1. ¿Qué es un armónico en función del tiempo?

Un armónico en función del tiempo es una señal que se repite periódicamente a lo largo del tiempo, y cuyas componentes frecuenciales son múltiplos enteros de una frecuencia fundamental.

2. ¿Cómo puedo calcular los armónicos en función del tiempo utilizando MATLAB?

Para calcular los armónicos en función del tiempo utilizando MATLAB, puedes utilizar la función fft para obtener la transformada de Fourier de la señal, y luego utilizar la función abs para obtener los valores de amplitud de cada armónico.

3. ¿Qué información puedo obtener al calcular los armónicos en función del tiempo?

Al calcular los armónicos en función del tiempo, puedes obtener información sobre las componentes frecuenciales presentes en una señal, como las frecuencias de los armónicos y sus amplitudes relativas.

4. ¿Es posible visualizar los armónicos en función del tiempo con MATLAB?

Sí, es posible visualizar los armónicos en función del tiempo utilizando MATLAB. Puedes utilizar la función plot para graficar la amplitud de cada armónico en función del tiempo.

5. ¿Qué aplicaciones pueden tener los armónicos en función del tiempo?

Los armónicos en función del tiempo tienen aplicaciones en diversas áreas, como el procesamiento de señales, la música, la física y la ingeniería. Por ejemplo, se utilizan en análisis de vibraciones, síntesis de sonido y en el estudio de fenómenos periódicos.