Aprende cómo hacer el ajuste lineal por mínimos cuadrados en MATLAB

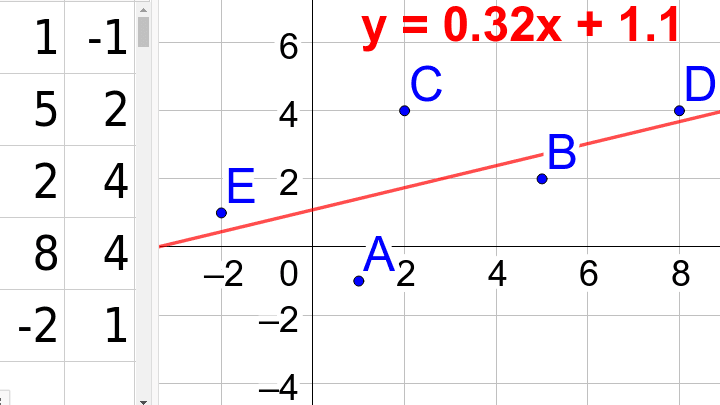
El ajuste lineal por mínimos cuadrados es una técnica muy útil en el análisis de datos para encontrar la mejor recta que se ajusta a un conjunto de puntos. MATLAB es una herramienta poderosa que ofrece varios métodos para realizar este ajuste de manera sencilla y eficiente. Si quieres aprender cómo utilizar MATLAB para realizar el ajuste lineal por mínimos cuadrados, este artículo te dará una guía paso a paso.

Te explicaré cómo realizar el ajuste lineal por mínimos cuadrados en MATLAB. Comenzaré explicándote brevemente en qué consiste este método y cómo se puede aplicar para ajustar una recta a un conjunto de puntos. Luego, te mostraré cómo utilizar la función polyfit de MATLAB para obtener los coeficientes de la recta de ajuste. Además, te enseñaré cómo realizar la visualización de los datos y la recta de ajuste utilizando la función plot. Si estás interesado en aprender cómo utilizar MATLAB para realizar el ajuste lineal por mínimos cuadrados, ¡sigue leyendo!

Cuáles son los fundamentos teóricos del método de mínimos cuadrados en el ajuste lineal

El método de mínimos cuadrados en el ajuste lineal es una técnica fundamental en el análisis numérico. Se basa en encontrar la línea recta que mejor se ajusta a un conjunto de datos y minimiza la suma de los errores al cuadrado entre los puntos y la línea.

Para obtener la ecuación de la recta, se utiliza el principio de la regresión lineal, que establece que la mejor línea recta que se ajusta a los datos debe tener la menor suma de los cuadrados de las diferencias entre los valores y los valores previstos por la línea recta.

Este método es ampliamente utilizado en diversas disciplinas, como la estadística, la econometría y la ingeniería. También es muy común utilizar el software MATLAB para realizar el cálculo del ajuste lineal por mínimos cuadrados debido a su facilidad de uso y su capacidad para realizar cálculos matemáticos eficientemente.

En el método de mínimos cuadrados, se utiliza la fórmula del ajuste lineal, que es:

y = mx + b

Donde y es la variable dependiente, x es la variable independiente, m es la pendiente de la recta y b es el término de intersección.

El objetivo del método de mínimos cuadrados es encontrar los valores de m y b que minimizan la suma de los cuadrados de las diferencias entre los valores de y y los valores previstos por la recta. Esto se logra mediante el cálculo de las derivadas parciales de la función objetivo con respecto a m y b, y resolviendo el sistema de ecuaciones resultante.

Una vez obtenidos los valores de m y b, se puede utilizar la ecuación de la recta para predecir los valores de y correspondientes a nuevos valores de x. Esto es especialmente útil en el análisis de datos en el que se desea hacer una predicción o extrapolar los resultados a un rango más amplio de valores.

El método de mínimos cuadrados en el ajuste lineal es una técnica poderosa para encontrar la mejor línea recta que se ajusta a un conjunto de datos. MATLAB proporciona una herramienta fácil de usar para realizar este cálculo, lo que lo convierte en una opción popular entre los investigadores y profesionales en diversas disciplinas.

Cuál es la importancia del ajuste lineal por mínimos cuadrados en el análisis de datos

El ajuste lineal por mínimos cuadrados es una técnica fundamental en el análisis de datos. Permite obtener una aproximación lineal de un conjunto de puntos, lo cual es especialmente útil cuando se desea modelar la relación entre dos variables.

Esta técnica es ampliamente utilizada en áreas como la estadística, la física, la economía y la ingeniería. Permite obtener una recta que mejor se ajuste a los datos disponibles, minimizando la suma de los cuadrados de las diferencias entre los valores observados y los estimados.

El uso del ajuste lineal por mínimos cuadrados puede proporcionar información valiosa, como la pendiente y la intersección de la recta de ajuste, que permiten interpretar el comportamiento de las variables analizadas.

El ajuste lineal por mínimos cuadrados es una herramienta esencial en el análisis de datos que proporciona una manera robusta de modelar y entender la relación entre variables.

Cuál es la fórmula matemática utilizada en el método de mínimos cuadrados para calcular los coeficientes de la línea de ajuste

En el método de mínimos cuadrados, se utiliza una fórmula matemática para calcular los coeficientes de la línea de ajuste. Esta fórmula se basa en el principio de minimizar la suma de los cuadrados de las diferencias entre los valores observados y los valores predichos por la línea de ajuste.

La fórmula para calcular el coeficiente de la pendiente (m) es:

m = (n Σ(xy) - Σx Σy) / (n Σ(x^2) - (Σx)^2)

Donde n es el número de puntos, Σ(xy) es la suma de los productos de las coordenadas x e y, Σx es la suma de las coordenadas x, Σy es la suma de las coordenadas y, y Σ(x^2) es la suma de los cuadrados de las coordenadas x.

Una vez que se ha calculado el coeficiente de la pendiente, el coeficiente de la intersección (b) se puede calcular utilizando la siguiente fórmula:

b = (Σy - m Σx) / n

Esta fórmula utiliza los mismos términos que la fórmula para el coeficiente de la pendiente.

Cómo se implementa el ajuste lineal por mínimos cuadrados en MATLAB

El ajuste lineal por mínimos cuadrados es una técnica muy utilizada en análisis de datos. En MATLAB, esta técnica puede implementarse de manera sencilla mediante el uso de la función polyfit(). Esta función calcula los coeficientes del polinomio de ajuste lineal que mejor se ajusta a los datos proporcionados.

Para utilizar la función polyfit() en MATLAB, primero es necesario tener los datos de entrada. Estos datos deben estar almacenados en dos vectores, uno para las coordenadas x y otro para las coordenadas y. Una vez que los datos están listos, se puede llamar a la función polyfit() pasando como argumentos los vectores de entrada y el grado del polinomio deseado.

La función polyfit() devuelve los coeficientes del polinomio de ajuste lineal en forma de un vector. El primer elemento de este vector corresponde al coeficiente de la variable de mayor grado, el segundo elemento corresponde al coeficiente de la variable de grado inferior, y así sucesivamente. Con estos coeficientes, se puede construir la ecuación del polinomio de ajuste lineal.

Una vez que se tiene la ecuación del polinomio de ajuste lineal, se puede utilizar para predecir valores de salida para nuevas entradas. En MATLAB, esto se puede hacer utilizando la función polyval(). Esta función toma como argumentos la ecuación del polinomio de ajuste lineal y los valores de entrada para los cuales se desea predecir los valores de salida.

El ajuste lineal por mínimos cuadrados en MATLAB puede implementarse fácilmente utilizando las funciones polyfit() y polyval(). Estas funciones permiten calcular los coeficientes del polinomio de ajuste lineal y realizar predicciones basadas en estos coeficientes. El ajuste lineal por mínimos cuadrados es una herramienta muy útil en análisis de datos y MATLAB proporciona las herramientas necesarias para implementarlo de manera eficiente.

Cuáles son las ventajas de utilizar MATLAB para el ajuste lineal por mínimos cuadrados

El ajuste lineal por mínimos cuadrados es una técnica estadística fundamental para encontrar la mejor línea de ajuste a un conjunto de datos. En este proceso, MATLAB ofrece varias ventajas que lo convierten en una herramienta poderosa y eficiente.

En primer lugar, MATLAB proporciona una amplia gama de funciones matemáticas y estadísticas que facilitan el cálculo de los coeficientes de regresión y los errores asociados. Esto permite realizar el ajuste lineal con facilidad y precisión.

Además, MATLAB ofrece una interfaz intuitiva y amigable que facilita la manipulación de los datos y la visualización de los resultados. Esto permite analizar y comprender fácilmente los resultados del ajuste lineal, lo que es especialmente útil para la toma de decisiones en investigación y desarrollo.

Otra ventaja significativa de utilizar MATLAB es su capacidad para manejar grandes conjuntos de datos de manera eficiente. Esto es especialmente importante cuando se trabaja con conjuntos de datos complejos y de gran escala, ya que MATLAB optimiza los algoritmos y utiliza el poder de procesamiento de la computadora de manera efectiva.

Por último, MATLAB es ampliamente utilizado en la comunidad científica e industrial, lo que significa que hay una gran cantidad de recursos, bibliotecas y herramientas disponibles. Esto facilita la colaboración, el aprendizaje y el intercambio de ideas entre investigadores y profesionales.

Utilizar MATLAB para el ajuste lineal por mínimos cuadrados ofrece una serie de ventajas significativas, como una amplia gama de funciones, una interfaz intuitiva, capacidad para manejar grandes conjuntos de datos y una comunidad activa de usuarios. Estas ventajas hacen de MATLAB una opción sólida y confiable para llevar a cabo este tipo de análisis estadístico.

Es posible realizar el ajuste lineal por mínimos cuadrados en MATLAB para datos no lineales

El ajuste lineal por mínimos cuadrados es una técnica ampliamente utilizada en el análisis de datos. MATLAB ofrece herramientas poderosas para llevar a cabo este tipo de ajuste, incluso en casos donde los datos no siguen una tendencia lineal.

Para realizar el ajuste lineal por mínimos cuadrados en MATLAB, debemos seguir algunos pasos clave. Primero, debemos cargar nuestros datos en la interfaz de MATLAB utilizando una estructura de datos adecuada, como una matriz o un vector.

A continuación, utilizaremos la función polyfit para realizar el ajuste lineal. Esta función nos permite ajustar nuestros datos a una función lineal de la forma y = mx + b, donde m y b son los coeficientes de la recta.

Una vez que hemos realizado el ajuste lineal por mínimos cuadrados, podemos utilizar la función polyval para evaluar la recta ajustada en puntos adicionales o para trazar la recta sobre los datos originales.

Es importante tener en cuenta que, aunque el ajuste lineal por mínimos cuadrados puede ser útil en muchos casos, también puede haber situaciones donde los datos no sigan una tendencia lineal clara. En estos casos, es posible que necesitemos considerar otras técnicas de ajuste, como el ajuste polinomial o el ajuste por mínimos cuadrados ponderados.

MATLAB nos ofrece una herramienta poderosa y flexible para realizar el ajuste lineal por mínimos cuadrados, incluso en datos no lineales. Con las funciones polyfit y polyval, podemos obtener los coeficientes de la recta ajustada y evaluarla en nuevos puntos. Sin embargo, es importante tener en cuenta que el ajuste lineal por mínimos cuadrados puede no ser siempre la mejor opción, dependiendo de la naturaleza de los datos.

Qué hacer si el ajuste lineal por mínimos cuadrados en MATLAB no se ajusta correctamente a los datos

Si estás teniendo problemas al ajustar tus datos utilizando el método de mínimos cuadrados en MATLAB, aquí te presentamos algunas posibles soluciones. Primero, asegúrate de que tus datos sean adecuados para un ajuste lineal. Si tus puntos de datos no siguen una tendencia lineal, es posible que necesites considerar un método de ajuste diferente.

Otra posible causa de un ajuste incorrecto es el ruido en los datos. Si tus datos contienen ruido, puedes intentar aplicar técnicas de suavizado antes de realizar el ajuste. Esto podría incluir el promedio de los datos o aplicar un filtro de paso bajo para eliminar las altas frecuencias.

Además, asegúrate de que estás utilizando la función de ajuste correcta en MATLAB. MATLAB ofrece varias funciones de ajuste lineal, como "polyfit" y "lsqcurvefit". Asegúrate de estar utilizando la función adecuada para tu tipo de ajuste.

También es importante verificar que estás proporcionando los argumentos correctos a la función de ajuste. Revisa la documentación de MATLAB para asegurarte de que estás ingresando los datos en el formato adecuado.

Finalmente, si ninguna de estas soluciones parece resolver el problema, considera buscar ayuda en la comunidad de MATLAB. Puedes publicar tu pregunta en los foros de MATLAB y recibir ayuda de otros usuarios experimentados.

Recuerda que el ajuste lineal por mínimos cuadrados es una herramienta poderosa, pero requiere un cuidadoso manejo de los datos y la selección adecuada de parámetros. Con paciencia y perseverancia, podrás lograr un ajuste preciso y confiable utilizando MATLAB.

Existen otras técnicas de ajuste de curvas que se pueden utilizar en MATLAB

Además del ajuste lineal por mínimos cuadrados, MATLAB ofrece otras técnicas poderosas para ajustar curvas a conjuntos de datos. Una de estas técnicas es el ajuste polinomial, que permite ajustar una función polinomial a los datos para obtener una curva suave que los represente.

Otra técnica es el ajuste exponencial, que se utiliza cuando los datos siguen una tendencia exponencial. MATLAB permite ajustar una curva exponencial a los datos para visualizar y analizar mejor la tendencia.

Asimismo, el ajuste por potencias es una técnica útil cuando los datos siguen una relación potencial, en la que una variable depende de la otra elevada a una potencia. MATLAB facilita el ajuste de una curva de potencias a los datos para comprender y modelar esta relación.

Adicionalmente, MATLAB también ofrece técnicas de ajuste de curvas más avanzadas, como el ajuste de curvas sinusoidales, el ajuste de curvas logarítmicas y el ajuste de curvas polinómicas no lineales. Estas técnicas permiten modelar una amplia variedad de comportamientos de datos y obtener una representación más precisa.

A través de MATLAB se pueden utilizar diversas técnicas de ajuste de curvas, como el ajuste polinomial, el ajuste exponencial, el ajuste por potencias y muchas más. Estas técnicas permiten adaptarse a diferentes tipos de datos y obtener una representación más precisa de los mismos.

Es posible evaluar la calidad del ajuste lineal por mínimos cuadrados en MATLAB

El ajuste lineal por mínimos cuadrados es una técnica ampliamente utilizada para modelar relaciones lineales entre variables. MATLAB ofrece una función incorporada llamada polyfit que permite realizar este tipo de ajuste de manera rápida y sencilla. Sin embargo, evaluar la calidad del ajuste es igualmente importante para obtener resultados confiables.

Una forma común de evaluar la calidad del ajuste lineal es mediante el cálculo del coeficiente de determinación, también conocido como R-cuadrado. Este coeficiente proporciona una medida de qué tan bien se ajusta la línea de regresión a los datos observados. Un R-cuadrado cercano a 1 indica un ajuste excelente, mientras que un valor cercano a 0 indica un ajuste deficiente.

Otra métrica útil para evaluar la calidad del ajuste es el error estándar de la estimación (SEE). El SEE representa la desviación estándar de los residuos, es decir, la diferencia entre los valores observados y los valores predichos por el modelo de ajuste lineal. Un SEE más bajo indica una menor dispersión de los residuos y, por lo tanto, un mejor ajuste.

Además del R-cuadrado y el SEE, también es posible visualizar el ajuste lineal utilizando gráficos de dispersión y la línea de regresión. Estos gráficos permiten verificar visualmente si el modelo de ajuste se ajusta adecuadamente a los datos observados. Si los datos se dispersan alrededor de la línea de regresión de manera uniforme y sin patrones distintos, es probable que el ajuste sea bueno.

MATLAB proporciona herramientas poderosas para realizar el ajuste lineal por mínimos cuadrados. Evaluar la calidad del ajuste es crucial para obtener resultados confiables y se pueden utilizar métricas como el R-cuadrado y el SEE, así como gráficos de dispersión, para lograrlo. Asegúrate de utilizar estas herramientas efectivamente para evaluar tus ajustes lineales en MATLAB.

Cuáles son las aplicaciones prácticas del ajuste lineal por mínimos cuadrados en el campo de la ciencia y la ingeniería

El ajuste lineal por mínimos cuadrados es una técnica ampliamente utilizada en el campo de la ciencia y la ingeniería debido a sus numerosas aplicaciones prácticas. En primer lugar, esta técnica es utilizada para modelar y analizar datos experimentales, permitiendo obtener una mejor comprensión de los fenómenos observados y extrapolar resultados.

Además, el ajuste lineal por mínimos cuadrados se utiliza en la estimación de parámetros en modelos matemáticos complejos. Esto es especialmente útil en la ingeniería, donde se busca optimizar el rendimiento de sistemas físicos o procesos.

Otra aplicación importante de esta técnica es en la econometría, donde se utiliza para analizar y predecir fenómenos económicos y sociales. La relación lineal entre variables permite realizar análisis de regresión y pronósticos.

El ajuste lineal por mínimos cuadrados es una herramienta fundamental en el campo de la ciencia y la ingeniería, con aplicaciones en el análisis de datos experimentales, la estimación de parámetros y la predicción de fenómenos económicos y sociales.

Preguntas frecuentes (FAQ)

1. ¿Qué es el ajuste lineal por mínimos cuadrados?

El ajuste lineal por mínimos cuadrados es una técnica estadística que permite encontrar la mejor línea recta que se ajusta a un conjunto de puntos en un gráfico.

2. ¿Cuál es la fórmula para el ajuste lineal por mínimos cuadrados?

La fórmula para el ajuste lineal por mínimos cuadrados es y = mx + b, donde m es la pendiente de la línea y b es el término constante.

3. ¿Cuál es el propósito del ajuste lineal por mínimos cuadrados?

El propósito del ajuste lineal por mínimos cuadrados es encontrar la línea recta que mejor se ajusta a un conjunto de puntos, con el fin de poder realizar predicciones o estimaciones basadas en esos datos.

4. ¿Cómo se realiza el ajuste lineal por mínimos cuadrados en MATLAB?

En MATLAB, se puede realizar el ajuste lineal por mínimos cuadrados utilizando la función polyfit, que devuelve los coeficientes de la línea recta que mejor se ajusta a los puntos dados.

5. ¿Qué importancia tiene el ajuste lineal por mínimos cuadrados en la práctica?

El ajuste lineal por mínimos cuadrados es ampliamente utilizado en diferentes disciplinas, como la física, la economía y la ingeniería, ya que permite modelar y predecir comportamientos lineales en base a datos experimentales o históricos.