Aprende a implementar el algoritmo de k vecinos más cercanos en MATLAB

El algoritmo de k vecinos más cercanos es un método utilizado comúnmente en el campo del aprendizaje automático para clasificar objetos o predecir valores basados en su cercanía a otros puntos de datos. Este algoritmo es especialmente útil en problemas de clasificación, donde se busca asignar una etiqueta o categoría a una nueva muestra en función de las características de otras muestras ya etiquetadas.

Aprenderemos cómo implementar el algoritmo de k vecinos más cercanos en MATLAB, un lenguaje de programación y entorno de desarrollo ampliamente utilizado en el campo de la ciencia e ingeniería. Exploraremos el proceso paso a paso, desde la preparación y carga de los datos hasta la clasificación de nuevas muestras utilizando el algoritmo kNN. Además, también veremos cómo evaluar la precisión del modelo y cómo ajustar el valor de k para obtener mejores resultados.

Cuál es la idea principal detrás del algoritmo de k vecinos más cercanos

El algoritmo de k vecinos más cercanos (KNN) es un método de aprendizaje supervisado utilizado en clasificación y regresión. La idea principal detrás de este algoritmo es encontrar los "k" puntos más cercanos a un punto de prueba y asignarle una etiqueta basada en la mayoría de las etiquetas de esos vecinos cercanos.

En otras palabras, el algoritmo clasifica nuevos puntos de datos basándose en la similitud con otros puntos de datos previamente etiquetados. Esto se logra calculando la distancia entre el punto de prueba y todos los demás puntos de datos en el conjunto de entrenamiento. Los "k" puntos más cercanos son seleccionados y la etiqueta más común es asignada al punto de prueba.

El algoritmo de KNN es muy útil en situaciones donde los datos no siguen una distribución lineal clara y puede ser utilizado para resolver problemas de clasificación en diversas áreas como medicina, reconocimiento de voz, recomendación de películas, entre otros.

Cómo funciona el algoritmo de k vecinos más cercanos en MATLAB

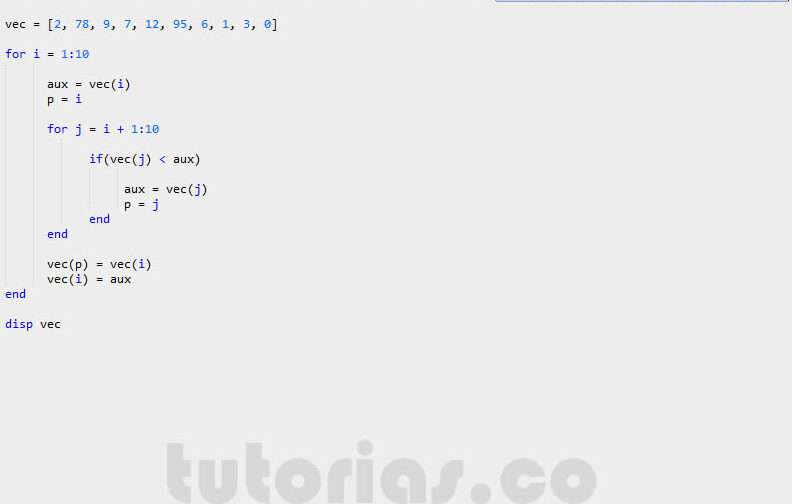
El algoritmo de k vecinos más cercanos es un método de aprendizaje automático supervisado que se utiliza para clasificación y regresión. En MATLAB, podemos implementar este algoritmo de manera sencilla utilizando algunas funciones y herramientas disponibles.

Primero, necesitaremos cargar nuestros datos de entrenamiento en MATLAB. Podemos almacenarlos en una matriz donde cada fila representa una instancia y cada columna representa una característica. Luego, dividimos nuestros datos en conjuntos de entrenamiento y prueba.

A continuación, debemos definir una función de distancia para medir cuán similares son dos instancias. Podemos utilizar la distancia euclidiana, la cual calcula la raíz cuadrada de la suma de los cuadrados de las diferencias entre las características.

Una vez que tenemos nuestra función de distancia, podemos comenzar con la clasificación propiamente dicha. Para cada instancia en el conjunto de prueba, calculamos su distancia a todas las instancias en el conjunto de entrenamiento.

Después de calcular las distancias, seleccionamos los k vecinos más cercanos a la instancia de prueba. Podemos ordenar las distancias y seleccionar los k primeros vecinos. Luego, determinamos la clase predominante entre estos vecinos y asignamos esa clase a la instancia de prueba.

Finalmente, podemos evaluar el rendimiento de nuestro algoritmo utilizando métricas como la precisión y el error cuadrático medio. Podemos comparar las clases asignadas por nuestro algoritmo con las clases reales del conjunto de prueba.

El algoritmo de k vecinos más cercanos es una técnica popular para la clasificación y regresión en aprendizaje automático. En MATLAB, podemos implementar este algoritmo siguiendo algunos pasos clave, que incluyen la carga y división de los datos, la definición de una función de distancia y la clasificación basada en los vecinos más cercanos.

Cuáles son las aplicaciones prácticas del algoritmo de k vecinos más cercanos

El algoritmo de k vecinos más cercanos, también conocido como k-NN, es ampliamente utilizado en el campo de la inteligencia artificial y el aprendizaje automático. Sus aplicaciones son diversas y se utilizan en numerosos sectores para resolver problemas de clasificación y regresión.

Una de las aplicaciones más comunes del algoritmo k-NN es en el ámbito de la recomendación de productos o servicios. Utilizando datos históricos de usuarios, el algoritmo puede identificar a qué grupo pertenece un nuevo usuario y recomendarle las opciones más adecuadas según su perfil.

Otro campo en el que el algoritmo k-NN es ampliamente utilizado es en la clasificación de imágenes. En este caso, se utiliza para identificar y categorizar imágenes en función de sus características visuales. Esto se utiliza en aplicaciones de reconocimiento facial, detección de objetos y muchas más.

Además, el algoritmo de k vecinos más cercanos también se utiliza en el campo de la medicina. Por ejemplo, se puede usar para clasificar pacientes en función de sus síntomas, permitiendo una mejor identificación de enfermedades y un tratamiento más eficiente.

Por último, el algoritmo k-NN también se utiliza en el campo de la finanzas, especialmente en la predicción de valores de acciones y en el análisis de riesgo. Utilizando datos históricos, el algoritmo puede identificar patrones y tendencias que ayudan en la toma de decisiones financieras.

El algoritmo de k vecinos más cercanos tiene una amplia gama de aplicaciones prácticas en diferentes campos, desde la recomendación de productos hasta el análisis de riesgo financiero. Su versatilidad y eficacia lo convierten en una herramienta valiosa en el ámbito del aprendizaje automático y la inteligencia artificial.

Es posible ajustar el valor de k en el algoritmo de k vecinos más cercanos

Cuando aplicamos el algoritmo de k vecinos más cercanos en MATLAB, uno de los parámetros clave es el valor de k. Este valor determina cuántos vecinos considerar al hacer la predicción de una muestra desconocida.

Para ajustar el valor de k, debemos tener en cuenta algunos factores importantes. Si elegimos un valor de k demasiado pequeño, es posible que la clasificación sea demasiado sensible a las fluctuaciones de los datos, lo que puede dar lugar a sobreajuste. Por otro lado, elegir un valor de k demasiado grande puede generar una clasificación más generalizada y menos precisa.

La elección del valor de k depende del conjunto de datos y del problema específico que estemos abordando. Una estrategia común es probar diferentes valores de k y evaluar el rendimiento del algoritmo utilizando alguna métrica de evaluación, como la precisión o el error. Esto nos permitirá encontrar el valor de k que mejor se ajuste a nuestro conjunto de datos.

En MATLAB, podemos ajustar el valor de k fácilmente modificando el código. Para ello, necesitamos definir una función que implemente el algoritmo de k vecinos más cercanos y que acepte el valor de k como un parámetro de entrada. Luego, podemos llamar a esta función con diferentes valores de k para evaluar el rendimiento del algoritmo.

El valor de k en el algoritmo de k vecinos más cercanos es un parámetro crucial que debe ajustarse cuidadosamente para obtener resultados precisos. Es importante considerar el equilibrio entre la sensibilidad y la generalización al elegir el valor de k. MATLAB facilita este proceso, ya que podemos ajustar el valor de k modificando el código y evaluando el rendimiento del algoritmo con diferentes valores.

Qué ventajas tiene implementar el algoritmo de k vecinos más cercanos en MATLAB

El algoritmo de k vecinos más cercanos es ampliamente utilizado en el campo del aprendizaje automático y la clasificación de datos. Implementarlo en MATLAB tiene varias ventajas.

En primer lugar, MATLAB es un lenguaje de programación muy versátil que permite un fácil manejo de matrices y cálculos numéricos, lo que facilita la implementación del algoritmo. Además, MATLAB cuenta con una amplia gama de funciones estadísticas y de aprendizaje automático integradas, lo que facilita la implementación de diferentes variantes y mejoras del algoritmo de k vecinos más cercanos.

Además, MATLAB tiene una interfaz gráfica amigable que facilita la visualización de los resultados y la evaluación de la precisión del algoritmo. Esto es especialmente útil cuando se trabaja con conjuntos de datos complejos y se necesitan herramientas visuales para entender y analizar los resultados.

Otra ventaja de implementar el algoritmo de k vecinos más cercanos en MATLAB es la velocidad de ejecución. MATLAB es conocido por su capacidad de procesamiento rápido y eficiente, lo que puede ser crucial cuando se trabaja con grandes conjuntos de datos o se requiere realizar múltiples iteraciones del algoritmo.

Implementar el algoritmo de k vecinos más cercanos en MATLAB ofrece ventajas en términos de facilidad de implementación, funcionalidad integrada, visualización de resultados y velocidad de ejecución. Es una opción sólida para aquellos que buscan desarrollar aplicaciones de aprendizaje automático y clasificación de datos de manera efectiva.

Cuáles son las limitaciones del algoritmo de k vecinos más cercanos en MATLAB

El algoritmo de k vecinos más cercanos es ampliamente utilizado en aprendizaje automático debido a su simplicidad y eficacia. Sin embargo, también tiene algunas limitaciones que es importante tener en cuenta al implementarlo en MATLAB.

Una de las principales limitaciones del algoritmo es su sensibilidad a la elección del valor de k. Un valor demasiado bajo puede resultar en un sobreajuste, mientras que un valor demasiado alto puede llevar a un subajuste. Es necesario encontrar el equilibrio adecuado para obtener resultados precisos.

Otra limitación es que el algoritmo asume que todas las características tienen la misma importancia. En algunos casos, ciertas características pueden ser más relevantes que otras, lo que podría afectar la precisión del modelo.

Además, el rendimiento del algoritmo puede verse afectado por la presencia de valores atípicos en los datos. Estos valores atípicos pueden distorsionar la distancia entre las muestras y afectar la elección de los vecinos más cercanos.

Por último, el algoritmo de k vecinos más cercanos puede ser computacionalmente costoso en términos de tiempo y memoria, especialmente cuando se trabaja con grandes conjuntos de datos. Esto puede limitar su aplicabilidad en ciertos escenarios.

A pesar de estas limitaciones, el algoritmo de k vecinos más cercanos sigue siendo una herramienta útil en muchos problemas de clasificación y regresión en MATLAB. Con un enfoque cuidadoso en la elección de k y el manejo de características, se pueden obtener resultados precisos y confiables.

Qué herramientas o bibliotecas de MATLAB se pueden utilizar para implementar el algoritmo de k vecinos más cercanos

Para implementar el algoritmo de k vecinos más cercanos en MATLAB, podemos utilizar diversas herramientas o bibliotecas que nos facilitarán el proceso.

1. Statistics and Machine Learning Toolbox

Esta es una biblioteca de MATLAB que proporciona funciones y algoritmos para el análisis estadístico y el aprendizaje automático. En particular, contiene varias funciones para realizar clasificación basada en el algoritmo de k vecinos más cercanos.

2. k-Nearest Neighbors Classification

Esta función específica de MATLAB implementa el algoritmo de k vecinos más cercanos para la clasificación de datos. Puede ser utilizada para clasificar nuevos datos en función de un conjunto de entrenamiento previamente etiquetado.

3. fitcknn

Esta función es parte de la toolbox de aprendizaje automático de MATLAB. Permite entrenar un modelo de k vecinos más cercanos utilizando un conjunto de datos de entrenamiento y etiquetas correspondientes. Luego, el modelo entrenado puede ser utilizado para clasificar nuevos datos.

4. ClassificationKNN

Esta clase de MATLAB implementa el algoritmo de k vecinos más cercanos para la clasificación de datos. Proporciona métodos para entrenar el modelo con un conjunto de entrenamiento y realizar predicciones sobre nuevos datos.

Estas son solo algunas de las herramientas y bibliotecas disponibles en MATLAB para implementar el algoritmo de k vecinos más cercanos. Dependiendo de tus necesidades y preferencias, puedes explorar y utilizar otras opciones que se ajusten mejor a tu problema específico.

Existen casos en los que el algoritmo de k vecinos más cercanos no sea la mejor opción

Si bien el algoritmo de k vecinos más cercanos es ampliamente utilizado y efectivo en muchos casos, existen situaciones en las que puede no ser la mejor opción. Por ejemplo, si tenemos un conjunto de datos con muchas dimensiones, el cálculo de las distancias puede volverse computacionalmente costoso y llevar mucho tiempo.

Además, el algoritmo de k vecinos más cercanos no tiene en cuenta la estructura subyacente de los datos, por lo que puede tener dificultades para capturar relaciones más complejas. Si los datos tienen una alta dimensionalidad y presentan una distribución no uniforme, podríamos obtener resultados menos precisos utilizando este algoritmo.

En estos casos, podría ser beneficioso considerar otras técnicas de aprendizaje automático, como el uso de árboles de decisión o redes neuronales, que pueden manejar mejor datos complejos y de alta dimensión. Es importante considerar cuidadosamente el contexto y las características de los datos antes de decidir implementar el algoritmo de k vecinos más cercanos en MATLAB.

Cuál es el tiempo de ejecución del algoritmo de k vecinos más cercanos en MATLAB en comparación con otros algoritmos de aprendizaje automático

El tiempo de ejecución del algoritmo de k vecinos más cercanos en MATLAB puede variar dependiendo del tamaño del conjunto de datos y la dimensión de los atributos. En general, el algoritmo de k vecinos más cercanos es considerado un algoritmo de clasificación lento en comparación con otros algoritmos de aprendizaje automático.

Esto se debe a que el algoritmo requiere calcular la distancia entre cada instancia del conjunto de entrenamiento y la instancia que se quiere clasificar. Además, el algoritmo debe ordenar las distancias para identificar los k vecinos más cercanos. Estas operaciones pueden ser costosas computacionalmente, especialmente cuando el conjunto de datos es grande.

En contraste, otros algoritmos de aprendizaje automático, como los árboles de decisión o las redes neuronales, pueden tener tiempos de ejecución más rápidos. Estos algoritmos suelen realizar operaciones más simples y eficientes en términos de tiempo de ejecución.

Sin embargo, es importante tener en cuenta que el tiempo de ejecución del algoritmo de k vecinos más cercanos en MATLAB puede optimizarse utilizando técnicas como el cálculo de distancias paralelo o el uso de estructuras de datos que aceleren la búsqueda de los vecinos más cercanos.

Hay alguna forma de mejorar la eficiencia del algoritmo de k vecinos más cercanos en MATLAB

Implementar el algoritmo de k vecinos más cercanos en MATLAB es relativamente sencillo, pero a veces puede ser necesario optimizar su eficiencia. Afortunadamente, existen algunas técnicas que pueden ayudarnos a mejorar el rendimiento de este algoritmo.

Una de las formas de mejorar la eficiencia es reduciendo la dimensionalidad de los datos de entrada. Si tenemos un conjunto de datos con muchas características, podemos utilizar técnicas de reducción de dimensionalidad como PCA (Análisis de Componentes Principales) para obtener una representación más compacta de los datos sin perder demasiada información.

Otra técnica que puede resultar útil es el uso de estructuras de datos eficientes para almacenar los datos de entrenamiento. En lugar de utilizar una matriz convencional, podemos utilizar una estructura de datos especializada para vecinos más cercanos, como un árbol KD (árbol de búsqueda k-dimensional) o un hash table, que nos permitirá buscar vecinos de manera más eficiente.

También es importante tener en cuenta la configuración de los parámetros del algoritmo. El valor de k, por ejemplo, debe ser elegido cuidadosamente. Un valor demasiado pequeño puede resultar en un sobreajuste, mientras que un valor demasiado grande puede resultar en un subajuste. Experimentar con diferentes valores de k puede ayudarnos a encontrar el equilibrio adecuado.

Además, podemos considerar la posibilidad de utilizar técnicas de preprocesamiento de datos, como la normalización o la estandarización, para mejorar la eficacia del algoritmo.

Si deseamos mejorar la eficiencia del algoritmo de k vecinos más cercanos en MATLAB, podemos utilizar técnicas como la reducción de dimensionalidad, el uso de estructuras de datos eficientes, la configuración adecuada de los parámetros y el preprocesamiento de datos. Estas técnicas nos ayudarán a obtener resultados más precisos y a mejorar el rendimiento general del algoritmo.

Qué parámetros se deben tener en cuenta al implementar el algoritmo de k vecinos más cercanos en MATLAB

Al implementar el algoritmo de k vecinos más cercanos en MATLAB, es importante considerar varios parámetros clave. En primer lugar, debes definir el valor de k, que representa el número de vecinos más cercanos a considerar. Un valor adecuado de k es crucial para obtener resultados precisos.

Otro parámetro importante es la métrica de distancia utilizada para calcular la cercanía entre los datos. MATLAB ofrece varias opciones, como la distancia euclidiana o la distancia de Manhattan. La elección de la métrica depende del problema y los datos específicos que estés tratando.

También debes prestar atención a la estrategia de ponderación utilizada en el algoritmo. Algunos enfoques ponderan a los vecinos más cercanos de manera uniforme, mientras que otros pueden asignar un peso mayor a los vecinos más cercanos. Esta elección puede influir en la precisión del algoritmo.

Además, es fundamental tener en cuenta si los datos requieren una normalización previa. A veces, los datos pueden tener diferentes escalas, lo que puede afectar la precisión del algoritmo. MATLAB ofrece funciones para normalizar los datos antes de aplicar el algoritmo de k vecinos más cercanos.

Pasos para implementar el algoritmo de k vecinos más cercanos en MATLAB

• Paso 1: Cargar los datos en MATLAB. Puedes utilizar funciones como "load" o "csvread" para importar tus datos.
• Paso 2: Preprocesar los datos si es necesario. Esto incluye normalizar los datos o eliminar atributos irrelevantes.
• Paso 3: Dividir los datos en conjuntos de entrenamiento y prueba. Puedes utilizar funciones como "crossvalind" o "cvpartition" para realizar la división.
• Paso 4: Implementar la función de cálculo de distancia. Puedes usar bucles para calcular la distancia entre cada par de puntos en los conjuntos de entrenamiento y prueba.
• Paso 5: Ordenar los vecinos más cercanos según la distancia calculada.
• Paso 6: Seleccionar los k vecinos más cercanos.
• Paso 7: Tomar una decisión basada en los vecinos seleccionados. Puedes utilizar varias estrategias, como la votación mayoritaria o el promedio de los valores.
• Paso 8: Evaluar la precisión del algoritmo utilizando los datos de prueba.

Implementar el algoritmo de k vecinos más cercanos en MATLAB puede ser una tarea desafiante, pero con estos parámetros y pasos clave, estarás en camino de lograr resultados precisos y efectivos para tu problema específico. Recuerda ajustar los parámetros y experimentar con diferentes enfoques para obtener los mejores resultados posibles. ¡Buena suerte!

Se puede utilizar el algoritmo de k vecinos más cercanos en problemas de clasificación y regresión en MATLAB

El algoritmo de k vecinos más cercanos (K-NN por sus siglas en inglés) es un método de aprendizaje automático supervisado que se utiliza tanto en problemas de clasificación como de regresión. En el caso de la clasificación, se emplea para asignar una etiqueta a una nueva instancia en función de las etiquetas de sus vecinos más cercanos. En la regresión, se utiliza para predecir un valor numérico basado en los valores de sus vecinos más cercanos.

En MATLAB, implementar el algoritmo de k vecinos más cercanos es sencillo y eficiente gracias a las funciones y herramientas que proporciona el software. En primer lugar, es necesario cargar los datos de entrenamiento y las etiquetas correspondientes. A continuación, se puede utilizar la función fitcknn para entrenar el modelo K-NN y la función predict para realizar predicciones sobre nuevos datos.

Antes de aplicar el algoritmo de k vecinos más cercanos, es importante realizar un preprocesamiento de los datos. Esto puede incluir la normalización de las características, la eliminación de valores atípicos y la selección de las características más relevantes. MATLAB ofrece diversas funciones y técnicas que facilitan este proceso, como normalize, removeoutliers y featureselection.

Una vez que el modelo ha sido entrenado y las predicciones han sido realizadas, es necesario evaluar su rendimiento. MATLAB proporciona varias métricas y herramientas para ello, como la matriz de confusión para problemas de clasificación y el error medio cuadrático para problemas de regresión. Estas métricas permiten determinar la precisión y la calidad de las predicciones del modelo K-NN.

Implementar el algoritmo de k vecinos más cercanos en MATLAB es una tarea accesible y eficiente gracias a las funciones y herramientas que ofrece el software. Con un adecuado preprocesamiento de los datos y una evaluación rigurosa del modelo, es posible obtener resultados precisos y confiables en problemas de clasificación y regresión.

Cuál es el impacto de la elección de la métrica de distancia en los resultados del algoritmo de k vecinos más cercanos en MATLAB

La elección de la métrica de distancia es un factor crítico en el algoritmo de k vecinos más cercanos en MATLAB. La métrica de distancia determina cómo se calcula la similitud entre las instancias de datos, lo cual afecta directamente los resultados del algoritmo.

Existen diferentes métricas de distancia disponibles en MATLAB, como la distancia euclidiana, la distancia de Manhattan y la distancia de Minkowski. Cada métrica tiene sus propias características y puede ser más adecuada según el tipo de datos y el problema específico.

La distancia euclidiana es la métrica más comúnmente utilizada, que calcula la distancia entre dos puntos en función de sus coordenadas. Es especialmente útil para datos numéricos y espaciales. Por otro lado, la distancia de Manhattan se calcula sumando las diferencias absolutas entre las coordenadas de los puntos, lo que la hace más adecuada para datos categóricos.

La métrica de Minkowski generaliza tanto la distancia euclidiana como la distancia de Manhattan, permitiendo ajustar un parámetro "p" que determina la forma de la distancia. Con p=2, la métrica de Minkowski es equivalente a la distancia euclidiana, mientras que con p=1, es equivalente a la distancia de Manhattan.

Es esencial que los científicos de datos evalúen y experimenten con diferentes métricas de distancia para encontrar la más adecuada para su conjunto de datos y objetivo. Esto puede lograrse utilizando la función "fitcknn" en MATLAB, que permite especificar la métrica de distancia deseada mediante el parámetro "Distance". Además, se puede utilizar la validación cruzada para comparar el rendimiento del algoritmo con diferentes métricas y seleccionar la mejor opción.

Existen alternativas al algoritmo de k vecinos más cercanos para resolver un problema similar en MATLAB

Si bien el algoritmo de k vecinos más cercanos es ampliamente utilizado para la clasificación y regresión en problemas de aprendizaje automático, no es la única opción disponible en MATLAB. Existen varias alternativas que pueden ser consideradas dependiendo de las características del problema y de los datos disponibles.

1. Árboles de decisión

Los árboles de decisión son una opción popular para la clasificación y regresión en MATLAB. Estos modelos utilizan una estructura de árbol para dividir los datos en diferentes ramas y tomar decisiones basadas en las características de los datos. Los árboles de decisión pueden ser especialmente útiles cuando los datos tienen características categóricas.

2. Máquinas de soporte vectorial

Las máquinas de soporte vectorial (SVM) son otro enfoque comúnmente utilizado en MATLAB. Estos modelos encuentran un hiperplano óptimo que separa los datos en diferentes clases. Las SVM pueden manejar tanto datos linealmente separables como no linealmente separables mediante el uso de diferentes funciones de kernel.

3. Redes neuronales

Las redes neuronales son un enfoque poderoso y flexible para la clasificación y regresión en MATLAB. Estos modelos están inspirados en el funcionamiento del cerebro humano y consisten en capas de neuronas interconectadas. Las redes neuronales pueden adaptarse a patrones complejos en los datos y pueden ser especialmente efectivas cuando se tienen grandes conjuntos de datos.

4. Random Forests

Los Random Forests son una combinación de árboles de decisión que se utilizan para la clasificación y regresión en MATLAB. Estos modelos generan múltiples árboles de decisión y promedian sus predicciones para obtener una predicción final. Los Random Forests pueden manejar datos con características faltantes y reducir el sobreajuste común en los árboles de decisión individuales.

5. Redes bayesianas

Las redes bayesianas son una opción popular para la clasificación en MATLAB. Estos modelos utilizan teoría de probabilidad y estadística para representar las relaciones entre las variables de los datos. Las redes bayesianas son especialmente útiles cuando se tienen datos con incertidumbre y se desea modelar la dependencia entre las variables.

Si bien el algoritmo de k vecinos más cercanos es una opción poderosa y ampliamente utilizada en MATLAB, no es la única alternativa disponible. Las alternativas mencionadas anteriormente, como los árboles de decisión, las máquinas de soporte vectorial, las redes neuronales, los Random Forests y las redes bayesianas, pueden ser consideradas dependiendo de las características del problema y de los datos disponibles.

Preguntas frecuentes (FAQ)

1. ¿Qué es el algoritmo de k vecinos más cercanos?

El algoritmo de k vecinos más cercanos es un método de clasificación que se basa en la cercanía entre los puntos de datos. Consiste en asignar a un nuevo punto la etiqueta de la clase más común entre sus k vecinos más cercanos.

2. ¿Cuál es la ventaja de utilizar el algoritmo de k vecinos más cercanos?

Una de las principales ventajas del algoritmo de k vecinos más cercanos es su simplicidad y facilidad de implementación. Además, es un algoritmo no paramétrico, lo que significa que no hace suposiciones sobre la distribución de los datos.

3. ¿Cómo se selecciona el valor de k en el algoritmo de k vecinos más cercanos?

La elección del valor de k en el algoritmo de k vecinos más cercanos depende del problema específico y debe ser seleccionada cuidadosamente. Un valor muy pequeño de k puede llevar a una clasificación demasiado sensible al ruido, mientras que un valor muy grande puede llevar a una clasificación demasiado generalizada.

4. ¿Es necesario normalizar los datos antes de aplicar el algoritmo de k vecinos más cercanos?

Dependiendo de la escala y la naturaleza de los datos, puede ser recomendable normalizarlos antes de aplicar el algoritmo de k vecinos más cercanos. La normalización ayuda a evitar que las características con escalas grandes dominen la clasificación.

5. ¿Cuáles son las principales limitaciones del algoritmo de k vecinos más cercanos?

Algunas de las limitaciones del algoritmo de k vecinos más cercanos incluyen su sensibilidad al ruido, su dependencia de la elección de k y su ineficiencia computacional cuando se trabaja con grandes conjuntos de datos.