Aprende a estimar una recta con RANSAC en MATLAB de forma sencilla

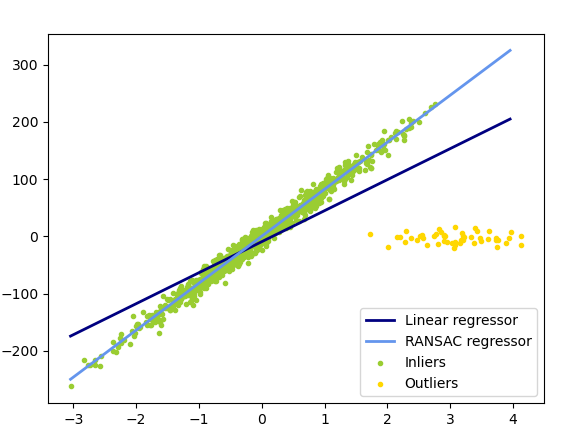
El proceso de estimar una recta a partir de puntos en un plano puede ser desafiante cuando existen outliers o puntos anómalos que no siguen el patrón general. En estos casos, resulta necesario utilizar algoritmos de estimación robusta que permitan obtener una aproximación más precisa de la recta deseada.

Te mostraré cómo utilizar el algoritmo RANSAC (Random Sample Consensus) en MATLAB para estimar una recta de manera sencilla. RANSAC es una técnica robusta que puede manejar de manera adecuada la presencia de puntos atípicos en el conjunto de datos, permitiéndonos obtener una estimación más robusta y confiable.

Qué es RANSAC y cómo se utiliza en la estimación de rectas en MATLAB

RANSAC (Random Sample Consensus) es un algoritmo utilizado para estimar parámetros de modelos matemáticos a partir de un conjunto de datos con ruido. En el caso de la estimación de rectas en MATLAB, RANSAC puede ser utilizado para encontrar la línea que mejor se ajusta a un conjunto de puntos.

El algoritmo de RANSAC funciona de la siguiente manera: se seleccionan aleatoriamente un número determinado de puntos del conjunto de datos y se calcula la línea que pasa por ellos. Luego, se comprueba cuántos puntos del conjunto original están suficientemente cerca de esta línea. Si el número de puntos cercanos supera un umbral predefinido, la línea se considera una buena estimación y se guarda. Este proceso se repite un número determinado de veces para obtener múltiples estimaciones.

El uso de RANSAC en la estimación de rectas en MATLAB presenta varias ventajas. Por un lado, es capaz de manejar conjuntos de datos con valores atípicos, ya que estos puntos aleatorios son menos propensos a ser seleccionados. Por otro lado, al generar múltiples estimaciones, el algoritmo puede considerar diferentes combinaciones de puntos, lo que aumenta la robustez y precisión de los resultados.

Cuáles son los pasos necesarios para implementar RANSAC en MATLAB para estimar una recta

Implementar el algoritmo RANSAC en MATLAB para estimar una recta es un proceso sencillo que consta de varios pasos clave. En este tutorial, te mostraré los pasos necesarios para lograrlo de forma efectiva.

Paso 1: Cargar los datos

Lo primero que debes hacer es cargar los datos necesarios para estimar la recta. Puedes hacerlo mediante un archivo CSV o simplemente ingresando los puntos manualmente.

Paso 2: Definir el modelo de recta

A continuación, debes definir el modelo de recta que utilizarás para estimar los datos. Esto implica seleccionar el tipo de recta (por ejemplo, lineal o polinómica) y determinar los parámetros que la caracterizan.

Paso 3: Implementar el algoritmo RANSAC

El siguiente paso consiste en implementar el algoritmo RANSAC en MATLAB. RANSAC es un algoritmo robusto que te permite estimar el modelo de recta incluso en presencia de datos atípicos.

Paso 4: Calcular el error

Una vez que hayas estimado la recta utilizando RANSAC, debes calcular el error asociado a dicha estimación. Esto te permitirá evaluar qué tan buen ajuste tiene tu modelo respecto a los datos reales.

Paso 5: Visualizar los resultados

Finalmente, es importante visualizar los resultados obtenidos. Puedes hacerlo mediante la generación de gráficas que muestren la recta estimada y los datos reales.

Ahora que conoces los pasos necesarios para implementar RANSAC en MATLAB y estimar una recta, estás listo para aplicarlo en tus propios proyectos. Recuerda que la clave está en cargar los datos, definir el modelo, implementar el algoritmo, calcular el error y visualizar los resultados. ¡Buena suerte!

Qué ventajas tiene RANSAC en comparación con otros algoritmos de estimación de rectas

RANSAC (Random Sample Consensus) es un algoritmo de estimación robusto ampliamente utilizado en visión por computadora y procesamiento de imágenes. Una de las ventajas principales de RANSAC es su capacidad para lidiar con datos que contienen valores atípicos o ruido. A diferencia de otros algoritmos de estimación de rectas, RANSAC es capaz de encontrar una solución aproximada incluso cuando una gran proporción de los puntos de datos están contaminados. Esto lo logra al seleccionar aleatoriamente un subconjunto de puntos para construir una línea y evaluar cuántos puntos se ajustan a esa línea. Si el número de puntos que se ajustan supera un umbral predeterminado, se considera un posible modelo de recta. De esta manera, RANSAC puede encontrar una buena aproximación de la recta real, ignorando los puntos atípicos o ruidosos.

Otra ventaja importante de RANSAC es su capacidad para manejar datos con incertidumbre. En lugar de asumir que todos los puntos de datos son precisos, RANSAC permite que ciertos puntos tengan errores o desviaciones. Esto es especialmente útil cuando se trabaja con datos obtenidos de sensores o dispositivos que pueden introducir cierto nivel de error en las mediciones. Al permitir la presencia de errores, RANSAC puede adaptarse mejor a situaciones del mundo real donde la precisión perfecta puede ser difícil de lograr.

Además, RANSAC es un algoritmo relativamente rápido y eficiente en comparación con otros métodos de estimación de rectas. Dado que selecciona aleatoriamente un subconjunto de puntos para construir una línea y solo evalúa el ajuste de los puntos seleccionados, RANSAC evita el cálculo exhaustivo de todas las combinaciones posibles de puntos. Esto lo hace especialmente útil cuando se trabaja con conjuntos de datos grandes o cuando se requiere una estimación en tiempo real.

Cuáles son las limitaciones y desafíos al utilizar RANSAC para estimar una recta en MATLAB

Utilizar RANSAC para estimar una recta en MATLAB puede ser una herramienta poderosa, pero también presenta ciertas limitaciones y desafíos a tener en cuenta. Uno de los principales desafíos es determinar los parámetros adecuados para el algoritmo RANSAC, como el número mínimo de puntos requeridos para considerar una línea válida.

Otra limitación es que RANSAC asume que los datos siguen un modelo lineal, lo que puede no ser válido en algunos casos. Si los datos tienen un comportamiento no lineal, la estimación de la recta puede resultar inexacta o incorrecta.

Además, utilizar RANSAC puede resultar computacionalmente costoso, especialmente cuando se tienen grandes conjuntos de datos. El algoritmo debe iterar múltiples veces para encontrar la mejor estimación, lo que puede llevar tiempo en casos de conjuntos de datos extensos.

Por último, RANSAC puede ser sensible a valores atípicos o ruido en los datos. Si existen valores atípicos significativos, es posible que RANSAC no pueda estimar correctamente la recta, lo que puede afectar la precisión de los resultados.

Existen paquetes o librerías específicas en MATLAB que faciliten la implementación de RANSAC para la estimación de rectas

Sí, en MATLAB existe una librería llamada Computer Vision System Toolbox que proporciona una función específica para implementar el algoritmo RANSAC para la estimación de rectas. Esta función se llama 'ransac' y se puede utilizar de manera sencilla para encontrar la mejor recta que se ajuste a un conjunto de puntos. Simplemente se le debe proporcionar una matriz de coordenadas (x, y) de los puntos y algunos parámetros como el número máximo de iteraciones y la tolerancia de error. A continuación, el algoritmo RANSAC seleccionará de manera automática los puntos inliers y estimará la recta que mejor se ajuste a ellos.

La función 'ransac' también devuelve los inliers y la ecuación de la recta estimada. Esto es muy útil para realizar tareas posteriores, como el trazado de la recta en una imagen o el cálculo de la distancia promedio entre los puntos y la recta estimada. Además, la librería Computer Vision System Toolbox también proporciona otras funciones relacionadas con la estimación de rectas, como 'fitline' que ajusta una recta a un conjunto de puntos dados utilizando métodos de ajuste de mínimos cuadrados.

Si estás buscando una manera sencilla de implementar RANSAC para la estimación de rectas en MATLAB, la librería Computer Vision System Toolbox te ofrece las herramientas necesarias. Puedes utilizar la función 'ransac' para obtener la mejor recta que se ajuste a tus datos, así como otras funciones para realizar tareas adicionales relacionadas con la estimación de rectas.

Cuáles son algunos ejemplos de aplicaciones prácticas donde la estimación de rectas con RANSAC en MATLAB es útil

La estimación de rectas con RANSAC en MATLAB es una herramienta muy útil en diversas aplicaciones prácticas. Por ejemplo, en el campo de la visión por computadora, se puede utilizar esta técnica para estimar líneas en imágenes y videos, lo que puede ser útil en tareas de detección de bordes, seguimiento de objetos y reconocimiento de formas.

Otra aplicación práctica donde esta técnica es útil es en la robótica. La estimación de rectas con RANSAC en MATLAB se puede utilizar para detectar y seguir líneas en el entorno, lo que puede ser útil en tareas de navegación autónoma de robots, como el seguimiento de líneas en pistas de carreras o el seguimiento de líneas en almacenes automatizados.

En el campo de la cartografía y la geodesia, la estimación de rectas con RANSAC en MATLAB también puede ser útil para estimar líneas en conjuntos de datos de puntos geográficos, lo que puede ser útil en tareas de mapeo y modelado del terreno.

Estos son solo algunos ejemplos de las muchas aplicaciones prácticas donde la estimación de rectas con RANSAC en MATLAB puede ser de gran utilidad. La flexibilidad y eficiencia de esta técnica la convierten en una herramienta esencial en el campo de la visión por computadora, la robótica y la cartografía.

Cuáles son algunas técnicas o estrategias que se pueden aplicar para mejorar la precisión y eficiencia de la estimación de rectas con RANSAC en MATLAB

Existen varias técnicas y estrategias que se pueden aplicar para mejorar la precisión y eficiencia de la estimación de rectas con RANSAC en MATLAB. A continuación, se presentarán algunas de las más utilizadas:

1. Ajuste de parámetros

Una de las primeras cosas a considerar es el ajuste de los parámetros del algoritmo RANSAC. Estos parámetros incluyen el umbral de distancia, el número mínimo de puntos para considerar un modelo válido y el número máximo de iteraciones. Ajustar estos parámetros de acuerdo con las características específicas del problema puede mejorar significativamente los resultados.

2. Eliminación de outliers

La presencia de outliers puede afectar negativamente la precisión de la estimación de rectas. Una estrategia común para lidiar con outliers es eliminarlos antes de aplicar el algoritmo RANSAC. Esto se puede hacer utilizando técnicas como el criterio de distancia Mahalanobis o el uso de modelos estadísticos robustos.

3. Mejora del modelo de ajuste

En algunos casos, el modelo de ajuste utilizado en el algoritmo RANSAC puede no ser lo suficientemente preciso para capturar las características de la recta. En tales casos, se puede considerar la utilización de modelos más complejos, como modelos polinómicos o modelos lineales generalizados, para mejorar la precisión de la estimación.

4. Utilización de técnicas de refinamiento

Después de obtener una estimación inicial de la recta con RANSAC, se puede aplicar técnicas de refinamiento para mejorar aún más la precisión. Estas técnicas incluyen el ajuste de mínimos cuadrados, que puede minimizar el error de la estimación, y la utilización de métodos de optimización numérica, como el método de Newton-Raphson, para encontrar la mejor recta que se ajuste a los puntos.

5. Evaluación de la calidad de la estimación

Es importante evaluar la calidad de la estimación de la recta obtenida con RANSAC. Esto se puede hacer mediante la utilización de métricas de evaluación, como el error medio cuadrático o el coeficiente de determinación. Si la calidad de la estimación no es satisfactoria, se pueden llevar a cabo ajustes adicionales o considerar la aplicación de diferentes técnicas de estimación.

6. Optimización del código

Por último, se puede mejorar la eficiencia de la estimación de rectas con RANSAC en MATLAB optimizando el código. Esto implica utilizar vectores y matrices en lugar de bucles for, aprovechar las funcionalidades de paralelización de MATLAB y minimizar el uso de recursos computacionales innecesarios. Una implementación eficiente del algoritmo puede reducir significativamente el tiempo de ejecución y mejorar la eficiencia global del proceso de estimación.

Aplicar técnicas de ajuste de parámetros, eliminación de outliers, mejora del modelo de ajuste, utilización de técnicas de refinamiento, evaluación de la calidad de la estimación y optimización del código puede permitir obtener estimaciones más precisas y eficientes de rectas con RANSAC en MATLAB.

Cómo se puede evaluar la calidad de la estimación de rectas obtenida utilizando RANSAC en MATLAB

La calidad de la estimación de rectas obtenida utilizando el algoritmo RANSAC en MATLAB puede ser evaluada de diferentes formas. Una de las métricas comunes utilizadas es el error promedio de la distancia entre los puntos y la recta estimada. Este error se calcula tomando la distancia de cada punto al modelo de recta y luego promediando los valores. Cuanto menor sea este valor, más precisa será la estimación de la recta.

Otra métrica popular para evaluar la calidad de la estimación de rectas es el coeficiente de determinación (R^2). Este coeficiente proporciona una medida de cuán bien se ajusta la recta de regresión a los datos. Un valor de R^2 cercano a 1 indica un buen ajuste, mientras que un valor cercano a 0 indica un mal ajuste.

También es posible evaluar la calidad de la estimación visualmente mediante la representación gráfica de la recta estimada junto con los puntos de datos. Esto permite observar si la recta se ajusta adecuadamente a los puntos, identificar posibles outliers y evaluar la dispersión de los datos alrededor de la recta estimada.

Error promedio de la distancia

El error promedio de la distancia es una métrica útil para evaluar la calidad de la estimación de rectas obtenida utilizando RANSAC en MATLAB. Esta métrica calcula la distancia de cada punto al modelo de recta estimada y promedia los valores obtenidos. Cuanto menor sea el error promedio de la distancia, más precisa será la estimación de la recta. Para calcular esta métrica, se puede utilizar la función "mean" de MATLAB junto con la función "distancia_punto_recta" que calcula la distancia entre un punto y una recta.

El código a continuación muestra cómo calcular el error promedio de la distancia utilizando RANSAC en MATLAB:


% Ejemplo de cálculo del error promedio de la distancia utilizando RANSAC en MATLAB

% Puntos de datos
datos = ;

% Estimación de la recta utilizando RANSAC
modelo_recta = estimar_recta_RANSAC(datos);

% Cálculo de la distancia de cada punto al modelo de recta
distancias = distancia_punto_recta(datos, modelo_recta);

% Cálculo del error promedio de la distancia
error_promedio_distancia = mean(distancias);

% Mostrar el resultado
disp();


Coeficiente de determinación (R^2)

El coeficiente de determinación (R^2) es otra métrica comúnmente utilizada para evaluar la calidad de la estimación de rectas obtenida utilizando RANSAC en MATLAB. Este coeficiente proporciona una medida de cuán bien se ajusta la recta de regresión a los datos. Un valor de R^2 cercano a 1 indica un buen ajuste, mientras que un valor cercano a 0 indica un mal ajuste.

El cálculo del coeficiente de determinación se puede realizar utilizando la función "corrcoef" de MATLAB. Esta función devuelve una matriz de coeficientes de correlación y podemos utilizar el segundo elemento de la diagonal de esta matriz para obtener el valor de R^2.

El código a continuación muestra cómo calcular el coeficiente de determinación utilizando RANSAC en MATLAB:


% Ejemplo de cálculo del coeficiente de determinación utilizando RANSAC en MATLAB

% Puntos de datos
datos = ;

% Estimación de la recta utilizando RANSAC
modelo_recta = estimar_recta_RANSAC(datos);

% Cálculo de los coeficientes de correlación
coeficientes_corr = corrcoef(datos(:, 1), datos(:, 2));

% Obtener el coeficiente de determinación
coeficiente_determinacion = coeficientes_corr(2)^2;

% Mostrar el resultado
disp();


Representación gráfica de la recta estimada

La representación gráfica de la recta estimada junto con los puntos de datos es otra forma de evaluar la calidad de la estimación de rectas obtenida utilizando RANSAC en MATLAB. Esta representación permite observar si la recta se ajusta adecuadamente a los puntos de datos, identificar posibles outliers y evaluar la dispersión de los datos alrededor de la recta estimada.

Para realizar la representación gráfica, se puede utilizar la función "plot" de MATLAB para trazar los puntos de datos y la recta estimada. Además, se puede utilizar la función "scatter" para resaltar los outliers detectados. Esto permite obtener una visualización clara de la calidad de la estimación de rectas.

El código a continuación muestra cómo realizar la representación gráfica de la recta estimada utilizando RANSAC en MATLAB:


% Ejemplo de representación gráfica de la recta estimada utilizando RANSAC en MATLAB

% Puntos de datos
datos = ;

% Estimación de la recta utilizando RANSAC
modelo_recta = estimar_recta_RANSAC(datos);

% Graficar los puntos de datos
scatter(datos(:, 1), datos(:, 2), 'b', 'filled');
hold on;

% Graficar la recta estimada
x = linspace(min(datos(:, 1)), max(datos(:, 1)), 100);
y = modelo_recta(1) x + modelo_recta(2);
plot(x, y, 'r', 'LineWidth', 2);

% Mostrar el resultado
legend('Puntos de datos', 'Recta estimada');
xlabel('X');
ylabel('Y');
title('Estimación de una recta utilizando RANSAC en MATLAB');


La calidad de la estimación de rectas obtenida utilizando RANSAC en MATLAB puede ser evaluada mediante métricas como el error promedio de la distancia y el coeficiente de determinación, así como mediante la representación gráfica de la recta estimada junto con los puntos de datos. Estas evaluaciones permiten determinar la precisión y el ajuste de la recta estimada, lo que resulta esencial en aplicaciones como el análisis de imágenes y la visión por computadora.

Cuáles son algunos recursos útiles, como tutoriales o documentación, para aprender más sobre la estimación de rectas con RANSAC en MATLAB

Si estás interesado en aprender más sobre cómo estimar una recta con RANSAC en MATLAB, hay algunos recursos útiles que puedes utilizar. Uno de ellos es el tutorial oficial de MathWorks sobre RANSAC, que proporciona una introducción detallada al algoritmo y cómo implementarlo en MATLAB.

Otra opción es consultar la documentación de MATLAB, donde podrás encontrar ejemplos de código y explicaciones paso a paso sobre cómo usar la función RANSAC para estimar una recta. Esta documentación incluye también ejercicios prácticos que te permitirán aplicar lo que has aprendido y poner a prueba tus habilidades.

Además, existen numerosos blogs y vídeos en línea que ofrecen tutoriales y explicaciones sobre cómo usar RANSAC en MATLAB para estimar rectas. Estos recursos pueden ser muy útiles para comprender mejor el algoritmo y su implementación en MATLAB, así como para aprender consejos y trucos adicionales para obtener mejores resultados.

Si estás interesado en aprender más sobre cómo estimar una recta con RANSAC en MATLAB, hay una variedad de recursos disponibles, como tutoriales oficiales, documentación de MATLAB y contenido en línea, que te ayudarán a profundizar en este tema y mejorar tus habilidades.

Qué otros algoritmos de estimación de rectas son populares en MATLAB y cómo se comparan con RANSAC en términos de precisión y eficiencia

Algoritmo de ajuste de mínimos cuadrados:

El algoritmo de ajuste de mínimos cuadrados es uno de los métodos más populares para estimar una recta en MATLAB. Este algoritmo minimiza la suma de los errores cuadrados entre los puntos y la recta estimada. Sin embargo, este método es sensible a los valores atípicos, lo que puede afectar la precisión de la estimación.

Método de la regresión robusta:

El método de la regresión robusta es otra alternativa para estimar una recta en MATLAB. A diferencia de los mínimos cuadrados, este método asigna pesos diferentes a los puntos, lo que reduce el impacto de los valores atípicos. Sin embargo, este enfoque puede resultar menos eficiente en términos computacionales, especialmente cuando se manejan grandes conjuntos de datos.

RANSAC (Random Sample Consensus):

RANSAC es un algoritmo de estimación de rectas robusto y eficiente en términos computacionales. Utiliza una combinación de aleatoriedad y consenso para identificar la mejor recta que se ajusta a un conjunto de puntos. Esta técnica es especialmente útil cuando se trabaja con datos que contienen valores atípicos. Aunque RANSAC puede no ser tan preciso como los métodos de mínimos cuadrados o regresión robusta, ofrece un equilibrio óptimo entre precisión y eficiencia.

Comparación de precisión y eficiencia:

En términos de precisión, el método de mínimos cuadrados puede proporcionar estimaciones más precisas cuando no hay valores atípicos presentes en los datos. Sin embargo, cuando los datos contienen valores atípicos, RANSAC y la regresión robusta pueden producir estimaciones más robustas y confiables.

En cuanto a eficiencia, RANSAC se destaca por su rapidez en comparación con los métodos de mínimos cuadrados y regresión robusta, especialmente cuando se trabaja con conjuntos de datos grandes. Esto se debe a que RANSAC utiliza una muestra aleatoria de puntos, en lugar de considerar todos los puntos, lo que reduce significativamente el tiempo de ejecución.

Si la precisión es primordial y no hay presencia de valores atípicos, los mínimos cuadrados pueden ser la mejor opción. Sin embargo, si se requiere una estimación robusta y eficiente, especialmente en presencia de valores atípicos, RANSAC es una elección óptima en MATLAB.

Preguntas frecuentes (FAQ)

1. ¿Qué es RANSAC?

RANSAC es un algoritmo robusto para estimar modelos matemáticos a partir de datos con ruido.

2. ¿Cómo funciona RANSAC?

RANSAC funciona seleccionando aleatoriamente un subconjunto de datos y ajustando un modelo a ese subconjunto. Luego, se evalúa cuántos puntos se ajustan a ese modelo y se repite el proceso varias veces para encontrar el mejor modelo.

3. ¿Para qué se utiliza RANSAC?

RANSAC se utiliza en problemas de estimación de modelos en presencia de datos atípicos o ruido. Es ampliamente utilizado en la visión por computadora y el procesamiento de imágenes.

4. ¿Cuáles son las ventajas de usar RANSAC?

Las ventajas de RANSAC incluyen su capacidad para manejar datos con ruido y outliers, su eficiencia computacional y su facilidad de implementación.

5. ¿Cómo puedo implementar RANSAC en MATLAB?

En MATLAB, puedes implementar RANSAC utilizando funciones como 'ransac' o 'fitgeotrans'. Estas funciones te permiten estimar modelos como rectas, círculos o homografías utilizando RANSAC.