Aprende a ajustar nube de puntos a un polinomio con MATLAB
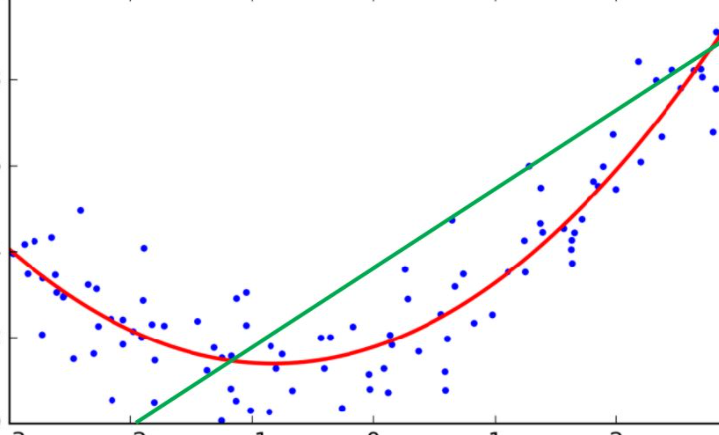
En el campo de la ciencia y la tecnología, es común encontrarse con datos que se presentan en forma de nube de puntos. Estas nubes de puntos pueden ser representaciones gráficas de mediciones, experimentos o cualquier tipo de toma de datos. Para poder analizar y modelar estos datos, es necesario ajustar estos puntos a ecuaciones matemáticas que permitan obtener una función que los describa de manera adecuada.
Aprenderás cómo ajustar una nube de puntos a un polinomio utilizando MATLAB, una poderosa herramienta de programación y análisis numérico. Exploraremos los pasos necesarios para realizar este ajuste, así como las funciones y comandos necesarios para llevarlo a cabo. Además, veremos ejemplos de cómo aplicar este método en diferentes situaciones y cómo interpretar los resultados obtenidos.
¿Qué verás en este artículo?
- Cuál es la importancia de ajustar una nube de puntos a un polinomio
- Cuáles son los pasos necesarios para ajustar una nube de puntos a un polinomio
- Qué es el método de mínimos cuadrados y cómo se aplica en el ajuste de nubes de puntos a polinomios
- Cuál es la función polyfit en MATLAB y cómo se utiliza para ajustar una nube de puntos a un polinomio
- Existen otras funciones en MATLAB que se pueden utilizar para ajustar una nube de puntos a un polinomio
- Cómo se determina el grado del polinomio al ajustar una nube de puntos en MATLAB
- Cuáles son las limitaciones y consideraciones al ajustar una nube de puntos a un polinomio en MATLAB
- Es posible ajustar una nube de puntos a un polinomio no lineal en MATLAB
- Qué tipos de aplicaciones y problemas pueden resolverse utilizando el ajuste de nubes de puntos a polinomios en MATLAB
- Cuáles son las mejores prácticas para visualizar y validar el ajuste de una nube de puntos a un polinomio en MATLAB
- Existen herramientas adicionales en MATLAB que se pueden utilizar para mejorar el ajuste de una nube de puntos a un polinomio
- Cuáles son los casos en los que el ajuste de una nube de puntos a un polinomio puede no ser la mejor opción y qué alternativas existen en MATLAB
- Preguntas frecuentes (FAQ)
Cuál es la importancia de ajustar una nube de puntos a un polinomio
Ajustar una nube de puntos a un polinomio es una técnica utilizada en análisis de datos y modelado matemático. Esta técnica permite encontrar una función polinómica que mejor se ajuste a los datos disponibles, lo que facilita el análisis y la predicción de valores futuros.
Este proceso es especialmente útil cuando se trabaja con datos que presentan una tendencia o patrón que se puede aproximar mediante una función polinómica. Al ajustar la nube de puntos a un polinomio, es posible obtener coeficientes que describen la forma específica de la función, lo que brinda información valiosa para el análisis y la toma de decisiones.
Además, el ajuste de una nube de puntos a un polinomio puede ayudar a identificar relaciones entre variables y predecir comportamientos futuros. Al tener una función polinómica que se ajuste bien a los datos disponibles, es posible utilizarla para realizar proyecciones y generar modelos que permitan realizar predicciones con mayor precisión.
Cuáles son los pasos necesarios para ajustar una nube de puntos a un polinomio
Para ajustar una nube de puntos a un polinomio utilizando MATLAB, hay varios pasos que debes seguir. En primer lugar, debes tener tus datos almacenados en dos matrices, una para las coordenadas x y otra para las coordenadas y. Luego, debes usar la función "polyfit" de MATLAB para ajustar el polinomio a tus datos. Esta función devolverá los coeficientes del polinomio ajustado. Después de obtener los coeficientes, puedes usar la función "polyval" para evaluar el polinomio en diferentes puntos o trazar la curva ajustada utilizando la función "plot".
Es importante mencionar que el grado del polinomio a ajustar dependerá de tus datos y del nivel de ajuste que desees obtener. En general, un polinomio de grado más alto se ajustará mejor a los datos, pero también podría llevar a un sobreajuste.
Paso 1: Preparar los datos
Antes de ajustar una nube de puntos a un polinomio en MATLAB, es necesario organizar los datos en dos matrices, una para las coordenadas x y otra para las coordenadas y. Asegúrate de que las matrices tengan las mismas dimensiones y que los valores estén ordenados correctamente.
Paso 2: Ajustar el polinomio
Una vez que tengas tus datos preparados, puedes utilizar la función "polyfit" de MATLAB para ajustar el polinomio. Esta función toma como argumentos las matrices de coordenadas x e y, así como el grado del polinomio deseado. Por ejemplo, si deseas ajustar un polinomio de grado 2, utilizarías la siguiente sintaxis: coeficientes = polyfit(x, y, 2). La función devolverá un vector con los coeficientes del polinomio ajustado.
Paso 3: Evaluar el polinomio
Una vez que hayas obtenido los coeficientes del polinomio ajustado, puedes utilizar la función "polyval" para evaluar el polinomio en diferentes puntos. Por ejemplo, si deseas evaluar el polinomio en el punto x = 5, utilizarías la siguiente sintaxis: y_evaluado = polyval(coeficientes, 5). La función devolverá el valor de y correspondiente al punto x = 5 en el polinomio ajustado.
Paso 4: Graficar el polinomio ajustado
Para visualizar el polinomio ajustado en relación con los datos originales, puedes utilizar la función "plot" de MATLAB. Esta función toma como argumentos las coordenadas x e y, así como los coeficientes del polinomio ajustado. Por ejemplo, si tus datos están almacenados en las matrices x e y, y los coeficientes del polinomio ajustado en el vector coeficientes, utilizarías la siguiente sintaxis: plot(x, y, 'o', x, polyval(coeficientes, x)). La función trazará los puntos de datos originales y la curva correspondiente al polinomio ajustado.
Recuerda que ajustar una nube de puntos a un polinomio puede ser útil en diferentes áreas, como ajuste de curvas, análisis de datos y modelado matemático. MATLAB proporciona las herramientas necesarias para realizar este tipo de ajustes de forma rápida y efectiva.
Qué es el método de mínimos cuadrados y cómo se aplica en el ajuste de nubes de puntos a polinomios
El método de mínimos cuadrados es una técnica utilizada para ajustar una función matemática a un conjunto de datos experimentales. En el contexto del ajuste de nubes de puntos a polinomios, este método es especialmente útil, ya que permite encontrar una curva suave que se ajuste de manera óptima a los datos disponibles.
En términos simples, el método de mínimos cuadrados busca minimizar la suma de los cuadrados de las diferencias entre los valores reales y los valores predichos por la función ajustada. Para ello, se utiliza un polinomio de grado n como función de ajuste, donde n es el grado del polinomio.
Para aplicar este método en MATLAB, existen varias funciones y enfoques disponibles. Una opción es utilizar la función polyfit, la cual ajusta un polinomio a una nube de puntos mediante el método de mínimos cuadrados polinomiales.
El proceso de ajuste se realiza en dos etapas: primero, se obtienen los coeficientes del polinomio utilizando la función polyfit; luego, se evalúa el polinomio ajustado en los puntos de interés utilizando la función polyval.
Es importante tener en cuenta que el grado del polinomio debe seleccionarse cuidadosamente, ya que un grado demasiado alto puede llevar a un sobreajuste de los datos, mientras que un grado demasiado bajo puede resultar en una mala aproximación.
El método de mínimos cuadrados es una herramienta poderosa para ajustar nubes de puntos a polinomios. MATLAB ofrece funciones como polyfit y polyval para facilitar este proceso y obtener resultados precisos. Al dominar este método, podrás realizar ajustes de manera eficiente y obtener curvas suaves que se ajusten fielmente a tus datos experimentales.
Cuál es la función polyfit en MATLAB y cómo se utiliza para ajustar una nube de puntos a un polinomio
La función polyfit en MATLAB es una herramienta poderosa que se utiliza para ajustar una nube de puntos a un polinomio. Este método se basa en el ajuste de mínimos cuadrados, que busca encontrar el polinomio que mejor se adapte a los datos proporcionados. Para utilizar esta función, se debe especificar el grado del polinomio deseado y los puntos de la nube a ajustar. Una vez ejecutado el comando, MATLAB devuelve los coeficientes del polinomio ajustado, que pueden ser utilizados para realizar predicciones o análisis adicionales.
El uso básico de la función polyfit es el siguiente:
coefficients = polyfit(x, y, degree);
Donde x y y son los vectores que contienen las coordenadas x e y de los puntos de la nube, respectivamente, y degree es el grado del polinomio deseado. Los coeficientes del polinomio ajustado se almacenan en el vector coefficients.
Es importante resaltar que, para obtener resultados precisos, es recomendable que la nube de puntos esté bien distribuida y contenga una cantidad suficiente de datos. Además, el grado del polinomio debe elegirse cuidadosamente, ya que un grado alto puede llevar a un ajuste excesivo o sobreajuste, mientras que un grado bajo puede conducir a un ajuste insuficiente o subajuste.
Existen otras funciones en MATLAB que se pueden utilizar para ajustar una nube de puntos a un polinomio
Además de la función polyfit, que hemos visto anteriormente, MATLAB ofrece otras opciones para ajustar una nube de puntos a un polinomio. Estas funciones adicionales proporcionan diferentes enfoques y métodos para obtener el mejor ajuste posible.
Función cftool
Una de las opciones más populares es utilizar la función cftool. Esta herramienta interactiva permite ajustar la nube de puntos a diferentes tipos de ajustes, incluyendo polinomios de diferentes grados, funciones trigonométricas y exponenciales, entre otras opciones.
Función fit
Otra opción es utilizar la función fit. Esta función permite ajustar la nube de puntos utilizando diferentes tipos de ajustes, incluyendo polinomios, funciones racionales, exponenciales y logarítmicas, entre otros. Además, la función fit también permite ajustar los datos a modelos personalizados creados por el usuario.
Función polyfitn
Si necesitas ajustar la nube de puntos a un polinomio multivariable, puedes utilizar la función polyfitn. Esta función extiende la funcionalidad de la función polyfit para ajustar polinomios de varias variables. Puedes especificar el grado del polinomio y los nombres de las variables en la función para obtener el mejor ajuste posible.
Como puedes ver, MATLAB ofrece diversas opciones para ajustar una nube de puntos a un polinomio. La elección de la función dependerá del tipo de ajuste que necesites realizar y de las características de tus datos. Experimenta con diferentes funciones y encuentra aquella que mejor se adapte a tus necesidades.
Cómo se determina el grado del polinomio al ajustar una nube de puntos en MATLAB
Al ajustar una nube de puntos a un polinomio en MATLAB, es fundamental determinar el grado adecuado del polinomio. El grado del polinomio determina la complejidad y precisión del ajuste. Si el grado es demasiado bajo, el polinomio no capturará adecuadamente la tendencia de los datos. Por el contrario, si el grado es demasiado alto, el polinomio se ajustará demasiado a los datos, lo que puede resultar en un sobreajuste.
Una forma común de determinar el grado adecuado del polinomio es utilizar la técnica del "ajuste de curvas". En esta técnica, se ajustan polinomios de diferentes grados a la nube de puntos y se evalúa la calidad del ajuste mediante métricas como el error cuadrático medio (MSE) o el coeficiente de determinación (R-squared). El grado óptimo del polinomio es aquel que minimiza el MSE o maximiza el R-squared.
En MATLAB, se puede utilizar la función polyfit para ajustar una nube de puntos a un polinomio de grado específico. Esta función utiliza el método de los mínimos cuadrados para encontrar los coeficientes del polinomio que mejor se ajustan a los datos. El grado del polinomio se especifica como argumento de entrada en la función polyfit.
Por ejemplo, si queremos ajustar una nube de puntos a un polinomio de grado 2 en MATLAB, podemos utilizar el siguiente código:
x = ;
y = ;
coefficients = polyfit(x, y, 2);
En este caso, la función polyfit ajustará una parábola (polinomio de grado 2) a la nube de puntos definida por los vectores x y y. Los coeficientes del polinomio resultante se almacenarán en el vector coefficients.
Consideraciones al determinar el grado del polinomio
No existe una regla fija para determinar el grado del polinomio en todos los casos. Dependerá de la naturaleza de los datos y el contexto del problema. Sin embargo, aquí hay algunas consideraciones que pueden ayudarte a tomar una decisión informada:
- Analiza la tendencia de los datos: Observa la forma general de la nube de puntos. Si parece tener una tendencia lineal, un polinomio de grado 1 probablemente sea suficiente. Si hay una curva evidente, es posible que un polinomio de grado mayor sea necesario.
- Evita el sobreajuste: Si el grado del polinomio es demasiado alto, es probable que el polinomio se ajuste demasiado a los datos y no capture la verdadera tendencia subyacente. Esto puede resultar en predicciones poco precisas para valores futuros.
- Utiliza métricas de ajuste: Evalúa la calidad del ajuste utilizando métricas como el MSE o el R-squared. Si el MSE disminuye o el R-squared aumenta significativamente al aumentar el grado del polinomio, podría ser un indicio de que el grado está mejorando el ajuste.
- Considera el costo computacional: A medida que aumenta el grado del polinomio, el costo computacional también aumenta. Si tienes un gran conjunto de datos, ajustar un polinomio de grado alto puede llevar mucho tiempo y requerir recursos adicionales.
Determinar el grado adecuado del polinomio al ajustar una nube de puntos en MATLAB es un proceso que requiere análisis y consideración. Es importante encontrar un equilibrio entre la complejidad del polinomio y su capacidad para capturar la tendencia de los datos. Utilizando técnicas como el ajuste de curvas y evaluando métricas de ajuste, puedes tomar decisiones informadas para obtener un ajuste óptimo.
Cuáles son las limitaciones y consideraciones al ajustar una nube de puntos a un polinomio en MATLAB
Al ajustar una nube de puntos a un polinomio en MATLAB, es importante tener en cuenta algunas limitaciones y consideraciones. En primer lugar, es fundamental seleccionar un grado adecuado para el polinomio de ajuste. Si el grado es demasiado alto, puede haber sobreajuste y el polinomio se adaptará demasiado a los puntos de datos, perdiendo la capacidad de generalizar. Por otro lado, si el grado es demasiado bajo, el polinomio puede no ser capaz de capturar la complejidad de los datos. Por lo tanto, es importante encontrar un equilibrio entre el ajuste y la complejidad del polinomio.
Otra consideración importante es el tipo de polinomio a utilizar. MATLAB ofrece diferentes tipos de polinomios, como el polinomio de Vandermonde, polinomio de Newton y polinomio de Lagrange. Cada uno tiene sus propias ventajas y desventajas, por lo que es importante entender cuál es el más adecuado para el problema específico que se está resolviendo.
Además, al ajustar una nube de puntos a un polinomio, es fundamental evaluar la calidad del ajuste. MATLAB proporciona herramientas para calcular el error de ajuste, como el error cuadrático medio. Este error permite cuantificar qué tan bien se ajusta el polinomio a los datos y ayuda a identificar posibles mejoras que puedan realizarse. También es importante tener en cuenta que el ajuste de una nube de puntos a un polinomio es una técnica determinista y puede no ser adecuada si los datos tienen ruido o errores.
Finalmente, es crucial considerar la interpretación de los resultados. Ajustar una nube de puntos a un polinomio puede proporcionar una función matemática que representa los datos, pero esto no necesariamente implica una relación causal entre las variables. Es importante utilizar el ajuste de polinomio como una herramienta exploratoria y complementar los resultados con análisis adicionales y conocimiento experto.
Es posible ajustar una nube de puntos a un polinomio no lineal en MATLAB
En el campo de la matemática y la programación, es común encontrarse con la necesidad de ajustar una nube de puntos a una función polinómica. MATLAB, uno de los lenguajes de programación más utilizados para el análisis de datos, ofrece numerosas herramientas para realizar este tipo de ajuste.
El ajuste de una nube de puntos a un polinomio no lineal implica encontrar la función polinómica que mejor se ajuste a los datos, minimizando el error entre los valores observados y los valores predichos por el polinomio. MATLAB ofrece un conjunto de funciones específicas para llevar a cabo este proceso, lo que facilita enormemente el trabajo de los programadores y analistas de datos.
El proceso de ajuste de la nube de puntos a un polinomio en MATLAB
El proceso de ajuste de una nube de puntos a un polinomio no lineal en MATLAB consta de varios pasos. Primero, se deben cargar los datos desde un archivo o generarlos de manera programática. Luego, se define el polinomio y se ajusta a los datos utilizando una función específica de MATLAB. Finalmente, se pueden realizar análisis adicionales y visualizar los resultados obtenidos.
- Cargar los datos: Los datos pueden provenir de diferentes fuentes, como archivos CSV o bases de datos. MATLAB proporciona funciones para leer estos datos y cargarlos en una matriz.
- Definir el polinomio: Una vez que los datos están cargados, se debe definir el polinomio con el que se ajustarán los puntos. Esto se puede hacer utilizando el comando "polyfit" de MATLAB. Se especifica el grado del polinomio y se obtienen los coeficientes correspondientes.
- Ajustar el polinomio a los datos: Con el polinomio definido, se utiliza la función "polyval" de MATLAB para ajustar los puntos a la curva polinómica. Esto implica calcular los valores predichos por el polinomio para cada punto de los datos.
- Análisis adicional: Una vez realizado el ajuste, se pueden realizar análisis adicionales para evaluar la calidad del ajuste. Esto incluye calcular el error residual, evaluar la bondad de ajuste y realizar pruebas estadísticas.
- Visualizar los resultados: Por último, se pueden visualizar los resultados obtenidos mediante la generación de gráficos. MATLAB ofrece funciones para trazar la nube de puntos y la curva ajustada en el mismo gráfico, lo que permite una fácil visualización y comparación.
El ajuste de una nube de puntos a un polinomio no lineal en MATLAB es una tarea común en el análisis de datos y la investigación científica. La gran cantidad de herramientas y funciones disponibles en MATLAB facilita enormemente este proceso, permitiendo a los analistas de datos obtener resultados precisos y confiables de manera eficiente.
Aprender a ajustar una nube de puntos a un polinomio utilizando MATLAB es una habilidad valiosa para cualquier persona que trabaje con análisis de datos y modelado matemático. Con las herramientas y funciones adecuadas, es posible realizar este tipo de ajuste de manera rápida y precisa, lo que permite tomar decisiones informadas basadas en los datos y obtener resultados confiables en diferentes campos de estudio.
Qué tipos de aplicaciones y problemas pueden resolverse utilizando el ajuste de nubes de puntos a polinomios en MATLAB
El ajuste de nubes de puntos a polinomios en MATLAB es una técnica muy versátil que puede aplicarse en una amplia gama de aplicaciones y problemas. Uno de los usos más comunes es en el campo de la interpolación, donde se utiliza para estimar valores desconocidos entre puntos conocidos en una serie de datos.
Además, el ajuste de nubes de puntos a polinomios también puede ser utilizado para modelar y predecir el comportamiento de fenómenos físicos, químicos o biológicos. Por ejemplo, se puede utilizar para ajustar datos de temperatura registrados en un experimento y así predecir la temperatura en un momento futuro.
Otro caso de uso común es en el análisis de datos financieros, donde el ajuste de nubes de puntos a polinomios se utiliza para modelar y predecir el comportamiento de los precios de las acciones o las tasas de interés. Esto permite a los analistas financieros tomar decisiones más informadas y realizar proyecciones a largo plazo.
El ajuste de nubes de puntos a polinomios en MATLAB es una herramienta poderosa que puede utilizarse en una amplia variedad de campos y problemas. Su flexibilidad y precisión lo convierten en una opción ideal para aquellos que buscan modelar datos, realizar predicciones y resolver problemas complejos.
Cuáles son las mejores prácticas para visualizar y validar el ajuste de una nube de puntos a un polinomio en MATLAB
El ajuste de una nube de puntos a un polinomio es una técnica ampliamente utilizada en análisis de datos y modelado. MATLAB ofrece herramientas poderosas para realizar esta tarea de manera eficiente y precisa. En este artículo, exploraremos las mejores prácticas para visualizar y validar el ajuste de una nube de puntos a un polinomio utilizando MATLAB.
¿Qué es una nube de puntos?
Una nube de puntos es una colección de puntos en un espacio multidimensional. Estos puntos pueden representar datos experimentales, mediciones o cualquier otra información que pueda ser expresada como coordenadas en un sistema de referencia. En el contexto de ajuste de polinomio, una nube de puntos representa una relación entre una variable independiente y una variable dependiente.
¿Por qué ajustar una nube de puntos a un polinomio?
Ajustar una nube de puntos a un polinomio nos permite encontrar una función que se ajuste de manera óptima a los datos observados. Esta función puede ser utilizada para predecir valores intermedios, extrapolar más allá de los datos observados o simplemente modelar la relación entre las variables. El ajuste de polinomio es una técnica flexible y ampliamente utilizada en diferentes áreas, como la física, la ingeniería y la ciencia de datos.
¿Cómo ajustar una nube de puntos a un polinomio en MATLAB?
En MATLAB, el ajuste de una nube de puntos a un polinomio se puede lograr utilizando la función "polyfit". Esta función utiliza el método de los mínimos cuadrados para encontrar los coeficientes del polinomio que mejor se ajusta a los datos. El resultado del ajuste es un vector de coeficientes que puede ser utilizado para evaluar la función polinómica en cualquier punto.
Visualización del ajuste de la nube de puntos
Una vez que hemos ajustado la nube de puntos a un polinomio en MATLAB, es importante visualizar el resultado para evaluar su calidad. Podemos utilizar la función "plot" para trazar los datos originales y la función polinómica ajustada en una gráfica. Comparar visualmente la nube de puntos y el ajuste polinómico nos permite identificar posibles discrepancias o patrones en los datos que pueden requerir ajustes adicionales.
Validación del ajuste de la nube de puntos
Además de la visualización, también es importante validar el ajuste de la nube de puntos a un polinomio en MATLAB. Podemos calcular el error residual, que es la diferencia entre los valores observados y los valores predichos por la función polinómica ajustada. Un error residual bajo indica un buen ajuste, mientras que un error residual alto puede sugerir que el polinomio no es el mejor modelo para los datos. MATLAB proporciona funciones como "residuals" y "norm" para calcular y evaluar el error residual.
El ajuste de una nube de puntos a un polinomio es una técnica valiosa en análisis de datos y modelado. MATLAB ofrece herramientas poderosas para realizar este ajuste de manera eficiente y precisa. Al visualizar y validar el ajuste, podemos evaluar la calidad del modelo y tomar decisiones informadas sobre su uso y aplicabilidad. Es importante recordar que el ajuste de polinomio es una herramienta flexible, pero puede no ser adecuado en todos los casos. La elección del grado del polinomio y la interpretación de los resultados son aspectos clave a considerar en el análisis de los datos.
Existen herramientas adicionales en MATLAB que se pueden utilizar para mejorar el ajuste de una nube de puntos a un polinomio
Una de esas herramientas es la función "polyfit", que permite ajustar una nube de puntos a un polinomio de grado determinado. Esta función utiliza el método de los mínimos cuadrados para encontrar el polinomio que mejor se ajusta a los datos.
El uso de "polyfit" es muy sencillo. Solo necesitas proporcionarle los vectores de coordenadas x e y de los puntos, así como el grado del polinomio que deseas ajustar. Por ejemplo, si deseas ajustar los puntos a un polinomio de grado 2, debes llamar a la función de la siguiente manera:
p = polyfit(x, y, 2);
Donde "p" será el vector que contendrá los coeficientes del polinomio ajustado.
Una vez que has obtenido los coeficientes del polinomio ajustado, puedes utilizar la función "polyval" para evaluar el polinomio en cualquier punto. Esta función también es muy sencilla de utilizar. Solo necesitas proporcionarle el vector de coeficientes del polinomio y el punto en el que deseas evaluarlo. Por ejemplo:
y_eval = polyval(p, x_eval);
Donde "y_eval" será el valor del polinomio evaluado en el punto "x_eval".
Además de estas funciones, MATLAB ofrece otras herramientas y funciones para el ajuste de nubes de puntos a polinomios, como "polyfitn" y "polyvaln", que permiten ajustar polinomios de múltiples variables. Estas herramientas son muy útiles para problemas más complejos donde los datos pueden depender de más de una variable.
MATLAB proporciona herramientas simples y poderosas para ajustar una nube de puntos a un polinomio. El uso de funciones como "polyfit" y "polyval" te permitirá obtener ajustes precisos y eficientes, sin la necesidad de escribir código complicado desde cero. ¡Aprovecha estas herramientas para mejorar tus análisis y modelos matemáticos!
Cuáles son los casos en los que el ajuste de una nube de puntos a un polinomio puede no ser la mejor opción y qué alternativas existen en MATLAB
Cuando trabajamos con una nube de puntos, es común querer ajustarla a un polinomio para obtener una representación más suave de los datos. Sin embargo, es importante tener en cuenta que hay casos en los que este enfoque puede no ser la mejor opción.
Una de las situaciones en las que el ajuste de una nube de puntos a un polinomio puede no ser adecuado es cuando los datos presentan un comportamiento no lineal o no siguen una tendencia polinomial clara. En tales casos, utilizar un polinomio puede producir un ajuste pobre y no representativo de los datos.
En lugar de utilizar un polinomio, MATLAB ofrece alternativas para ajustar nubes de puntos en casos más complejos. Una de ellas es el ajuste de una curva utilizando una función no polinomial, como una función exponencial o logarítmica. Esto permite capturar mejor las características no lineales de los datos.
Otra opción es utilizar métodos de ajuste no paramétricos, como la regresión no paramétrica o los splines. Estos métodos se basan en modelos más flexibles y pueden adaptarse mejor a datos complejos sin depender de una forma funcional específica.
El ajuste de una nube de puntos a un polinomio puede ser una buena opción en muchos casos, pero no siempre es la mejor alternativa. Para situaciones más complejas, MATLAB ofrece opciones más adecuadas, como ajustes de curvas no polinomiales o métodos de ajuste no paramétricos.
Preguntas frecuentes (FAQ)
1. ¿Qué es una nube de puntos?
Una nube de puntos es una colección de puntos en el espacio tridimensional que pueden representar datos obtenidos de mediciones o escaneos.
2. ¿Por qué ajustar una nube de puntos a un polinomio?
Ajustar una nube de puntos a un polinomio permite obtener una función matemática que se ajuste a los datos y permita realizar cálculos y análisis más precisos de los mismos.
3. ¿Cómo se ajusta una nube de puntos a un polinomio con MATLAB?
Se puede utilizar el comando "polyfit" de MATLAB para ajustar una nube de puntos a un polinomio. Este comando realiza una regresión polinómica para encontrar los coeficientes del polinomio de mejor ajuste.
4. ¿Es necesario conocer el grado del polinomio a ajustar de antemano?
Es recomendable tener una idea del grado del polinomio que se ajustará a la nube de puntos, sin embargo, MATLAB permite realizar ajustes con diferentes grados y luego analizar cuál proporciona un mejor ajuste.
5. ¿Cómo se evalúa el ajuste del polinomio a la nube de puntos?
Una forma de evaluar el ajuste del polinomio a la nube de puntos es calcular el error residual, que representa la diferencia entre los valores estimados por el polinomio y los valores reales de la nube de puntos. MATLAB proporciona funciones para calcular este error, como "polyval" y "rmse".
Calcula la derivada por definición en MATLAB: paso a paso
Añade columna al inicio de un vector en MATLAB: guía fácil y rápida
Conviértete en un experto: Cómo crear un array de 0 a 1 en MATLAB
Encuentra fácilmente el valor mínimo en un array cell en MATLAB
Abre tus ficheros de forma rápida y sencilla con este script de Matlab
Elimina archivos de una carpeta con Matlab de forma sencilla
Elevar 10 a un número en MATLAB: La guía definitiva sin complicaciones
Aprende fácilmente a calcular las soluciones de una función con MATLAB
Calcula la media de un vector en Matlab fácilmente paso a paso
Deja una respuesta
Artículos que podrían interesarte