
Ajusta una curva gaussiana con MATLAB: paso a paso
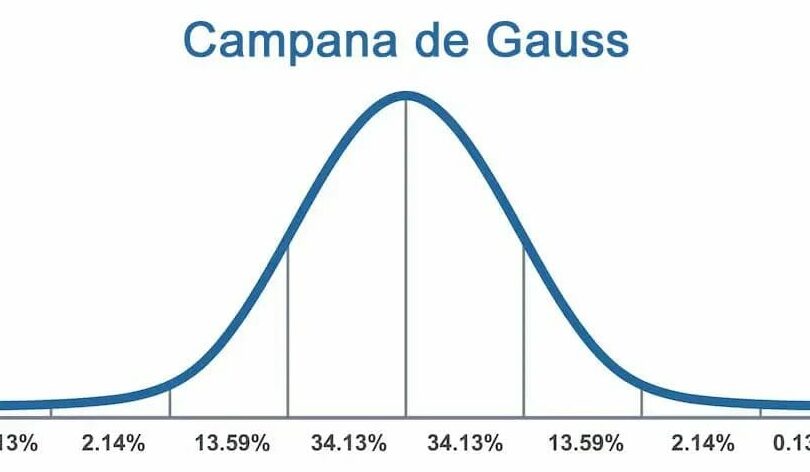
En el campo de la ciencia y la estadística, muchas veces nos encontramos con datos que siguen una distribución gaussiana o en forma de campana. La curva gaussiana, también conocida como curva normal, es una función matemática que describe la distribución de valores alrededor de un valor medio. Ajustar una curva gaussiana a un conjunto de datos nos permite modelar y entender mejor el fenómeno que estamos estudiando.
Exploraremos cómo ajustar una curva gaussiana utilizando MATLAB, un software de programación y un entorno de desarrollo ampliamente utilizado en el ámbito científico. Veremos los pasos necesarios para importar los datos, ajustar la curva y visualizar los resultados. Además, discutiremos algunas consideraciones importantes a tener en cuenta al ajustar una curva gaussiana. ¡Prepárate para sumergirte en el fascinante mundo de las estadísticas y el análisis de datos con MATLAB!
- Cómo puedo ajustar una curva gaussiana a mis datos usando MATLAB
- Cuáles son los pasos necesarios para ajustar una curva gaussiana con MATLAB
- Es posible ajustar una curva gaussiana a un conjunto de datos que no sigue una distribución normal
- Qué métodos o funciones de MATLAB puedo utilizar para ajustar una curva gaussiana
- Cuál es la diferencia entre ajustar una curva gaussiana con el método de mínimos cuadrados y el método de máxima verosimilitud
- Cuáles son las ventajas y desventajas de ajustar una curva gaussiana a mis datos
- Cuáles son las aplicaciones más comunes de ajustar curvas gaussianas en MATLAB
- Cómo puedo evaluar la calidad del ajuste de mi curva gaussiana en MATLAB
- Existen paquetes o complementos de MATLAB que faciliten el ajuste de curvas gaussianas
- Qué debo tener en cuenta al ajustar una curva gaussiana a datos experimentales en MATLAB
- Preguntas frecuentes (FAQ)
Cómo puedo ajustar una curva gaussiana a mis datos usando MATLAB
Ajustar una curva gaussiana a los datos puede ser una tarea desafiante, pero MATLAB ofrece una solución sencilla y eficiente. Para empezar, necesitarás tener los datos almacenados en una matriz. Luego, debes utilizar la función fit de MATLAB, que te permite ajustar diversos tipos de curvas a tus datos.
Para ajustar una curva gaussiana específicamente, debes especificar el modelo gaussiano en la función fit. El modelo gaussiano está compuesto por una función exponencial y una distribución normal. En MATLAB, puedes utilizar la función gaussmf para representar la función exponencial y la distribución normal.
Una vez que hayas definido el modelo gaussiano, debes ajustar los parámetros para obtener los mejores resultados. En MATLAB, puedes utilizar la función cftool para interactuar con una interfaz gráfica que te permitirá ajustar los parámetros de manera visual. Alternativamente, si prefieres automatizar el proceso, puedes utilizar la función fit directamente y especificar los límites y valores iniciales para cada parámetro.
Una vez que hayas ajustado la curva gaussiana a tus datos, puedes utilizarla para realizar diversas operaciones de análisis. Por ejemplo, puedes utilizar la curva ajustada para predecir el valor de una variable desconocida o para calcular el área bajo la curva. MATLAB te ofrece una amplia gama de funciones para realizar estas operaciones de manera sencilla.
Ajustar una curva gaussiana a tus datos usando MATLAB es un proceso sencillo y eficiente. Solo necesitas tener tus datos en una matriz, definir el modelo gaussiano y ajustar los parámetros. Una vez ajustada la curva, puedes utilizarla para realizar diversas operaciones de análisis. MATLAB te ofrece todas las herramientas necesarias para este proceso, lo cual lo convierte en una opción ideal para este tipo de tareas.
Cuáles son los pasos necesarios para ajustar una curva gaussiana con MATLAB
Ajustar una curva gaussiana con MATLAB es un proceso que requiere seguir varios pasos. En primer lugar, se debe tener una idea clara de cómo se ve una curva gaussiana y qué parámetros la definen. Una curva gaussiana es una distribución de probabilidad continua que tiene la forma de una campana simétrica.
El primer paso para ajustar una curva gaussiana es tener los datos en MATLAB. Esto se puede hacer cargando un archivo de datos o ingresándolos manualmente en un vector. Una vez que los datos están disponibles, el siguiente paso es inicializar los parámetros de la curva gaussiana, como la media y la desviación estándar.
Para ajustar la curva gaussiana a los datos, MATLAB ofrece varias funciones, como "fitdist" y "normfit", que permiten estimar los parámetros de la curva gaussiana a partir de los datos. Estas funciones utilizan algoritmos de ajuste de máxima verosimilitud para encontrar los valores óptimos de los parámetros.
Paso 1: Preparar los datos
Antes de ajustar la curva gaussiana, es necesario asegurarse de que los datos sean apropiados para este tipo de distribución. Se deben eliminar los valores atípicos y comprobar que los datos sigan una distribución aproximadamente gaussiana.
Paso 2: Inicializar los parámetros
Una vez que los datos están listos, se deben inicializar los parámetros de la curva gaussiana. Esto implica establecer valores iniciales razonables para la media y la desviación estándar. Estos valores iniciales pueden ser estimaciones aproximadas basadas en el conocimiento del problema o en análisis exploratorios previos.
Paso 3: Ajustar la curva gaussiana
El paso principal consiste en ajustar la curva gaussiana a los datos utilizando una función de ajuste en MATLAB, como "fitdist". Esta función tomará los datos y devolverá los valores estimados de los parámetros de la curva gaussiana.
Paso 4: Evaluar el ajuste
Una vez que se ha ajustado la curva gaussiana, es importante evaluar la calidad del ajuste. Esto se puede hacer calculando el error cuadrático medio o visualizando la curva ajustada junto con los datos. Si el ajuste no es satisfactorio, es posible que sea necesario modificar los valores iniciales de los parámetros o probar con otro tipo de distribución.
Ajustar una curva gaussiana con MATLAB requiere seguir varios pasos, desde la preparación de los datos hasta el ajuste y evaluación del resultado. Con las funciones adecuadas y una comprensión clara de los pasos necesarios, es posible obtener un ajuste preciso y confiable de una curva gaussiana en MATLAB.
Es posible ajustar una curva gaussiana a un conjunto de datos que no sigue una distribución normal
La distribución gaussiana, también conocida como distribución normal, es una de las distribuciones más utilizadas en estadística debido a su simetría y su forma de campana. Sin embargo, en muchos casos, los datos recopilados no siguen una distribución normal. Afortunadamente, MATLAB ofrece una herramienta poderosa para ajustar una curva gaussiana a un conjunto de datos, incluso si no siguen una distribución normal.
El ajuste de la curva gaussiana implica encontrar los parámetros óptimos para que la curva se ajuste lo mejor posible a los datos. Estos parámetros incluyen la media (μ) y la desviación estándar (σ) de la distribución gaussiana. Una vez que se ha ajustado la curva, se puede utilizar para hacer predicciones y analizar los datos con mayor precisión.
Paso 1: Preparar los datos
Antes de comenzar a ajustar la curva gaussiana, es importante preparar los datos de manera adecuada. Esto implica limpiar los datos de cualquier ruido o valor atípico, así como también asegurarse de que los datos estén normalizados. Para ello, se pueden utilizar diversas técnicas en MATLAB, como filtrado y normalización de datos.
Paso 2: Definir la función gaussiana
Una vez que los datos están listos, es necesario definir la función gaussiana en MATLAB. La función gaussiana es una función matemática que describe la distribución de probabilidad de una variable aleatoria continua. En MATLAB, se puede definir la función gaussiana utilizando la siguiente expresión:
y = (1/(sqrt(2pisigma^2)))exp(-((x-mu)^2)/(2sigma^2))
Donde y es el valor de salida de la función gaussiana, x es la variable independiente, mu es la media y sigma es la desviación estándar.
Paso 3: Ajustar la curva gaussiana a los datos
Una vez que se ha definido la función gaussiana, se puede proceder a ajustarla a los datos utilizando la función fit en MATLAB. Esta función utiliza un algoritmo de ajuste de curva para encontrar los parámetros óptimos que minimizan la diferencia entre la curva ajustada y los datos reales. Para ajustar la curva gaussiana, se debe proporcionar la función gaussiana definida previamente, así como los datos de entrada.
El resultado del ajuste de la curva será un conjunto de parámetros que representan la media y la desviación estándar de la curva gaussiana ajustada. Estos parámetros pueden utilizarse para hacer predicciones y analizar los datos con mayor precisión.
Paso 4: Evaluar la calidad del ajuste
Una vez que se ha ajustado la curva gaussiana a los datos, es importante evaluar la calidad del ajuste. Esto implica calcular diversas métricas estadísticas, como el coeficiente de determinación (R²) y el error cuadrático medio (MSE), para determinar qué tan bien se ajusta la curva a los datos. MATLAB ofrece funciones integradas para calcular estas métricas y analizar la calidad del ajuste de la curva.
Ajustar una curva gaussiana a un conjunto de datos en MATLAB puede ser de gran utilidad en diversos campos, como la física, la química, la biología y la ingeniería. Con los pasos descritos anteriormente, puedes ajustar una curva gaussiana a tus propios datos y utilizarla para realizar predicciones y análisis más precisos.
Qué métodos o funciones de MATLAB puedo utilizar para ajustar una curva gaussiana
Para ajustar una curva gaussiana utilizando MATLAB, existen varias opciones disponibles. Una de las más comunes es utilizar la función "fitdist", que se encuentra en la Toolbox de Estadísticas de MATLAB. Esta función permite ajustar distintos tipos de distribuciones, incluyendo la gaussiana.
Otra opción es utilizar la función "normfit", que ajusta una distribución gaussiana a los datos proporcionados. Esta función devuelve los parámetros de la distribución ajustada, como la media y la desviación estándar.
Además, MATLAB también ofrece la función "gaussfit", que permite ajustar una curva gaussiana a un conjunto de datos proporcionados. Esta función utiliza un enfoque de mínimos cuadrados para encontrar los parámetros óptimos de la curva gaussiana.
Independientemente del método elegido, la clave para ajustar una curva gaussiana con MATLAB es tener los datos adecuados y utilizar las funciones adecuadas para el ajuste. Experimentar con diferentes opciones y ajustar los parámetros según sea necesario es fundamental para obtener resultados precisos y confiables.
Cuál es la diferencia entre ajustar una curva gaussiana con el método de mínimos cuadrados y el método de máxima verosimilitud
El ajuste de una curva gaussiana es un proceso común en el análisis de datos, pero existen diferentes métodos para lograrlo. Dos de los enfoques más utilizados son el método de mínimos cuadrados y el método de máxima verosimilitud.
El método de mínimos cuadrados busca encontrar los parámetros de la curva gaussiana que minimizan la suma de los cuadrados de las diferencias entre los valores reales y los valores predichos por la curva ajustada. Este método es ampliamente utilizado debido a su simplicidad y facilidad de implementación.
Por otro lado, el método de máxima verosimilitud busca encontrar los parámetros que maximizan la probabilidad de obtener los datos observados dados los parámetros de la curva gaussiana. Este enfoque tiene en cuenta la distribución estadística de los datos y ofrece una estimación más precisa de los parámetros.
El método de mínimos cuadrados es más adecuado cuando se desea un ajuste rápido y simplificado de la curva gaussiana, mientras que el método de máxima verosimilitud es más apropiado cuando se requiere una estimación más precisa y se considera la distribución estadística de los datos.
Cuáles son las ventajas y desventajas de ajustar una curva gaussiana a mis datos
Ajustar una curva gaussiana a los datos puede proporcionar numerosas ventajas en la interpretación de los resultados. Una de las principales ventajas es que permite modelar de manera precisa la distribución de los datos. Esto es especialmente útil cuando se trabaja con datos que siguen una distribución normal, ya que la curva gaussiana se ajusta perfectamente a este tipo de distribución.
Además, el ajuste de una curva gaussiana puede ayudar a estimar parámetros estadísticos importantes, como la media y la desviación estándar de los datos. Estos parámetros son fundamentales en el análisis de datos y pueden proporcionar información valiosa sobre la tendencia central y la dispersión de los datos.
Otra ventaja del ajuste de una curva gaussiana es que puede facilitar la comparación de diferentes conjuntos de datos. Al ajustar una curva gaussiana a cada conjunto de datos, es posible obtener parámetros comparables y evaluar cuál de los conjuntos de datos se ajusta mejor a una distribución normal.
Sin embargo, también existen algunas desventajas en el ajuste de una curva gaussiana. En primer lugar, este método asume que los datos siguen una distribución normal, lo cual puede ser incorrecto en algunos casos. En tales situaciones, el ajuste de una curva gaussiana puede llevar a conclusiones equivocadas.
Otra desventaja es que el ajuste de una curva gaussiana puede ser computacionalmente costoso, especialmente cuando se tienen grandes conjuntos de datos. Esto significa que el proceso de ajuste puede llevar mucho tiempo y requerir una gran cantidad de recursos computacionales.
El ajuste de una curva gaussiana puede proporcionar muchas ventajas al analizar y modelar datos. Sin embargo, es importante tener en cuenta las limitaciones y considerar si este método es adecuado para los datos en cuestión.
Cuáles son las aplicaciones más comunes de ajustar curvas gaussianas en MATLAB
El ajuste de curvas gaussianas es una técnica utilizada comúnmente en aplicaciones de procesamiento de señales, análisis de datos y modelado estadístico. Esta técnica tiene varias aplicaciones, como el análisis de espectros de señales, la detección de picos en datos experimentales y la estimación de parámetros en modelos estadísticos. En el campo de la investigación científica, el ajuste de curvas gaussianas se utiliza para analizar los resultados de experimentos y estudios. Esta técnica es ampliamente utilizada en diversas disciplinas y es una herramienta poderosa para el análisis de datos.
Cómo puedo evaluar la calidad del ajuste de mi curva gaussiana en MATLAB
Al ajustar una curva gaussiana con MATLAB, es importante evaluar la calidad del ajuste para asegurarnos de que los resultados obtenidos son confiables. Hay varias métricas que podemos utilizar para evaluar la calidad del ajuste de una curva gaussiana.
Residuos
Una forma común de evaluar la calidad del ajuste es mediante el análisis de los residuos. Los residuos son la diferencia entre los valores observados y los valores predichos por el ajuste de la curva gaussiana. Podemos graficar los residuos y verificar si siguen una distribución normal alrededor de cero. Si los residuos son aleatorios y se distribuyen normalmente, esto indica un buen ajuste.
Coeficiente de determinación (R-squared)
Otra métrica comúnmente utilizada es el coeficiente de determinación, también conocido como R-squared. El coeficiente de determinación nos indica qué tan bien los valores observados se ajustan a la curva ajustada. Un valor de R-squared cercano a 1 indica un buen ajuste, mientras que un valor cercano a 0 indica un mal ajuste.
Chi-cuadrado
El chi-cuadrado es otra métrica utilizada para evaluar la calidad del ajuste de una curva gaussiana. El chi-cuadrado compara los valores observados con los valores esperados de acuerdo con el ajuste de la curva gaussiana. Un valor de chi-cuadrado pequeño indica un buen ajuste, mientras que un valor grande indica un mal ajuste.
Al ajustar una curva gaussiana en MATLAB, podemos evaluar la calidad del ajuste utilizando métricas como los residuos, el coeficiente de determinación y el chi-cuadrado. Estas métricas nos permiten asegurarnos de que los resultados obtenidos son confiables y que el ajuste es adecuado para nuestros datos.
Existen paquetes o complementos de MATLAB que faciliten el ajuste de curvas gaussianas
Sí, existen varios paquetes y complementos de MATLAB que facilitan el ajuste de curvas gaussianas. Uno de los más utilizados es el paquete Statistics and Machine Learning Toolbox, que proporciona funciones específicas para ajustar modelos estadísticos, como curvas gaussianas, a conjuntos de datos.
Además, MATLAB también ofrece la posibilidad de utilizar el comando fitdist para ajustar una distribución de probabilidad a un conjunto de datos, incluyendo la distribución gaussiana. Este comando permite ajustar la curva gaussiana a los datos de forma rápida y sencilla.
Otro paquete muy utilizado es el Curve Fitting Toolbox, que permite ajustar curvas no lineales, incluyendo las gaussianas. Este paquete proporciona una interfaz gráfica intuitiva que facilita el ajuste de las curvas a los datos.
Estos paquetes y complementos de MATLAB son herramientas poderosas que facilitan el ajuste de curvas gaussianas y permiten obtener resultados precisos y confiables. Su uso es muy recomendado para aquellos que necesiten realizar este tipo de ajustes en sus análisis de datos.
Qué debo tener en cuenta al ajustar una curva gaussiana a datos experimentales en MATLAB
Al ajustar una curva gaussiana a datos experimentales en MATLAB, hay varios aspectos importantes a tener en cuenta. En primer lugar, es esencial comprender el concepto de una curva gaussiana y su función de densidad de probabilidad. La curva gaussiana se caracteriza por su forma de campana y es ampliamente utilizada para modelar distribuciones simétricas de datos.
Para ajustar una curva gaussiana a los datos experimentales, es necesario tener una comprensión sólida de las funciones y métodos disponibles en MATLAB. Una función útil es la función gaussiana, que se puede utilizar para generar datos sintéticos basados en una distribución gaussiana.
Uno de los enfoques más comunes para ajustar una curva gaussiana a datos reales es utilizar la función de ajuste de curva 'fit' de MATLAB. Esta función permite ajustar una curva gaussiana a los datos y proporciona una estimación de los parámetros de la curva, como la media y la desviación estándar.
Es importante tener en cuenta que el éxito del ajuste de la curva gaussiana depende en gran medida de la calidad de los datos experimentales. Los datos deben ser lo más precisos y completos posible para obtener resultados confiables. Además, es posible que sea necesario realizar algunas transformaciones previas a los datos, como la eliminación de valores atípicos o la normalización de los datos, para obtener un ajuste óptimo.
Una vez realizado el ajuste de la curva gaussiana, es importante evaluar la calidad del ajuste utilizando métricas como el coeficiente de determinación (R-cuadrado) o el error cuadrático medio (MSE). Estas métricas proporcionan una medida de qué tan bien la curva ajustada se ajusta a los datos experimentales.
Al ajustar una curva gaussiana a datos experimentales en MATLAB, es esencial comprender los conceptos básicos de las curvas gaussianas y tener un conocimiento sólido de las funciones y métodos disponibles en MATLAB. Además, se deben tener en cuenta las consideraciones sobre la calidad de los datos y evaluar la calidad del ajuste obtenido.
Preguntas frecuentes (FAQ)
1. ¿Qué es una curva gaussiana?
Una curva gaussiana, también conocida como distribución normal, es una función matemática que describe una campana simétrica alrededor de un valor central.
2. ¿Por qué es útil ajustar una curva gaussiana?
Ajustar una curva gaussiana es útil para modelar y analizar datos que siguen una distribución normal, lo cual es común en muchos campos de estudio, como la estadística y la física.
3. ¿Cómo puedo ajustar una curva gaussiana en MATLAB?
En MATLAB, puedes ajustar una curva gaussiana utilizando la función 'fitdist' del Toolbox de Estadísticas y Aprendizaje de Máquinas. Esta función permite estimar los parámetros de la distribución gaussiana a partir de los datos de entrada.
4. ¿Cuáles son los parámetros de una curva gaussiana?
Los parámetros de una curva gaussiana son la media (el valor central de la campana) y la desviación estándar (que determina qué tan ancha o estrecha es la campana).
5. ¿Qué puedo hacer con el ajuste de una curva gaussiana en MATLAB?
Una vez que tienes el ajuste de la curva gaussiana, puedes utilizar los parámetros estimados para realizar análisis estadísticos, pronósticos y predicciones basados en la distribución normal de tus datos.
Deja una respuesta








Artículos que podrían interesarte